题目内容
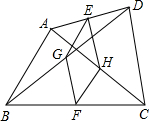 如图任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件________时,四边形EGFH是菱形.(填一个使结论成立的条件)
如图任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件________时,四边形EGFH是菱形.(填一个使结论成立的条件)
AB=CD
分析:E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH= CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
解答:需添加条件AB=CD.
证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG= AB同理HF∥AB,且HF=
AB同理HF∥AB,且HF= AB,
AB,
∴EG HF.
HF.
∴四边形EGFH是平行四边形.
∵EG= AB,
AB,
又可同理证得EH= CD,
CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为:AB=CD.
点评:本题主要考查了三角形中位线定理与菱性的判定方法,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.
分析:E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG
 HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH= CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.解答:需添加条件AB=CD.
证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG=
 AB同理HF∥AB,且HF=
AB同理HF∥AB,且HF= AB,
AB,∴EG
 HF.
HF.∴四边形EGFH是平行四边形.
∵EG=
 AB,
AB,又可同理证得EH=
 CD,
CD,∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为:AB=CD.
点评:本题主要考查了三角形中位线定理与菱性的判定方法,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.

练习册系列答案
相关题目
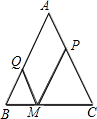 如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q. 25、已知:如图,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB,AC的平行线交AC于P,交AB于Q.
25、已知:如图,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB,AC的平行线交AC于P,交AB于Q. 如图,正三角形ABC内接于⊙O,P是劣弧BC上的任意一点,若PA=2,则四边形ABPC的面积为
如图,正三角形ABC内接于⊙O,P是劣弧BC上的任意一点,若PA=2,则四边形ABPC的面积为
 (2012•浦口区一模)提出问题:
(2012•浦口区一模)提出问题: ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.