题目内容
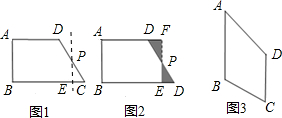
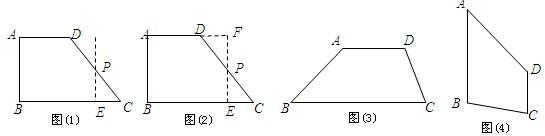
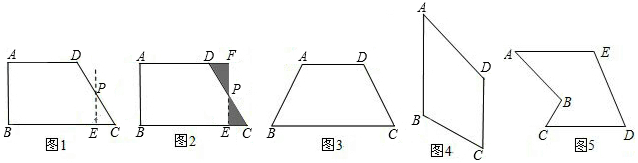
操作示例:(1)如图1,△ABC中,AD为BC边上的中线,△ABD的面积记为S△ABD,△ADC的面积记为S△ADC.则S△ABD=S△ADC.
(2)在图2中,E、F分别为四边形ABCD的边AD、BC的中点,四边形ABCD的面积记为S四边形ABCD,阴影部分面积记为S阴,则S阴和S四边形ABCD之间满足的关系式为:S阴=
| 1 | 2 |
解决问题:
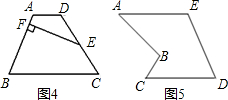
在图3中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和,并说明理由.
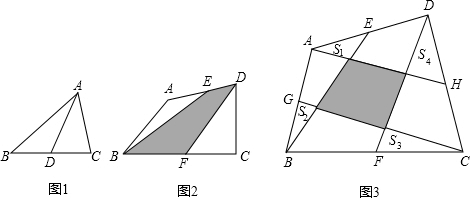
分析:先设空白处面积分别为:x、y、m、n,由上得 S四边形BEDF=
S四边形ABCD,S四边形AHCG=
S四边形ABCD,可得(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,然后S1+S2+S3+S4=S阴即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:设空白处面积分别为:x、y、m、n,由题意得
解:设空白处面积分别为:x、y、m、n,由题意得
S四边形BEDF=
S四边形ABCD,S四边形AHCG=
S四边形ABCD,
∴S1+x+S2+S3+y+S4=
S四边形ABCD,S1+m+S4+S2+n+S3=
S四边形ABCD,
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,
∴S1+S2+S3+S4=S阴=20平方厘米.
故四个小三角形的面积和为20平方厘米.
 解:设空白处面积分别为:x、y、m、n,由题意得
解:设空白处面积分别为:x、y、m、n,由题意得 S四边形BEDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S1+x+S2+S3+y+S4=
| 1 |
| 2 |
| 1 |
| 2 |
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,
∴S1+S2+S3+S4=S阴=20平方厘米.
故四个小三角形的面积和为20平方厘米.
点评:此题主要考查学生对三角形面积的理解和掌握,难点是需要分别求得S1、S2、S3、S4.然后S1+S2+S3+S4=S阴即可,这是此题的突破点.

练习册系列答案
相关题目
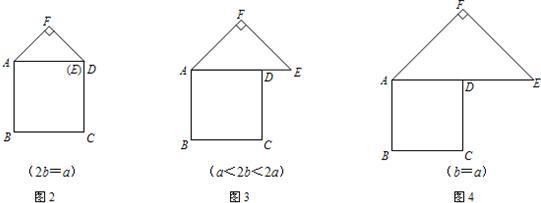
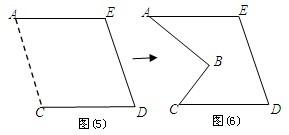
 25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.