题目内容
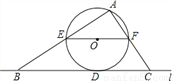
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 ______ .
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
题目内容
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 ______ .

 应用题作业本系列答案
应用题作业本系列答案