题目内容
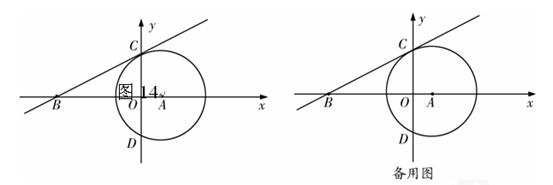
已知:如图14,⊙A与 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为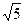 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0).
轴于点B(-4,0).(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.
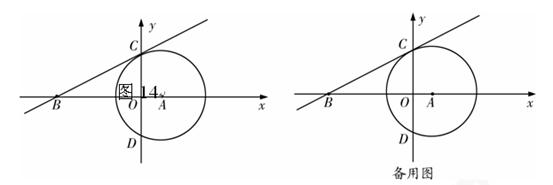
解:(1)如图1所示,连接AC,则AC=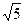

在Rt△AOC中,AC=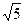 ,OA="1" ,则OC=2
,OA="1" ,则OC=2
∴点C的坐标为(0,2) ……………………….(1分)
设切线BC的解析式为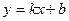 ,它过点C(0,2),B(?4,0),则有
,它过点C(0,2),B(?4,0),则有
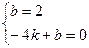 解之得
解之得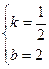
∴ ……………………….(2分)
……………………….(2分)
(2)如图1所示,设点G的坐标为(a,c),过点G作GH⊥ 轴,
轴,
垂足为H点,则OH="a," GH=c=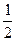 a + 2
a + 2
连接AP, AG
因为AC="AP" , AG="AG" , 所以Rt△ACG≌Rt△APG (HL)
所以∠AGC=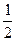 ×1200=600 ……………………….(3分)
×1200=600 ……………………….(3分)
在Rt△ACG中,∠AGC= 600,AC=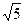
∴Sin600= ∴AG =
∴AG =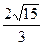 ……………………….(4分)
……………………….(4分)
在Rt△AGH中, AH=OH-OA=a-1 ,GH=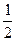 a+ 2
a+ 2

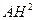 +
+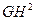 =
=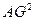
∴ +
+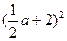 =
=
解之得: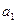 =
= ,
,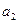 = ?
= ? (舍去) ……………………….(5分)
(舍去) ……………………….(5分)
点G的坐标为( ,
, + 2 ) ……………………….(6分) 解析:
+ 2 ) ……………………….(6分) 解析:
略
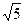

在Rt△AOC中,AC=
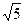 ,OA="1" ,则OC=2
,OA="1" ,则OC=2∴点C的坐标为(0,2) ……………………….(1分)
设切线BC的解析式为
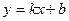 ,它过点C(0,2),B(?4,0),则有
,它过点C(0,2),B(?4,0),则有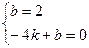 解之得
解之得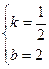
∴
 ……………………….(2分)
……………………….(2分)(2)如图1所示,设点G的坐标为(a,c),过点G作GH⊥
 轴,
轴,垂足为H点,则OH="a," GH=c=
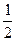 a + 2
a + 2 连接AP, AG
因为AC="AP" , AG="AG" , 所以Rt△ACG≌Rt△APG (HL)
所以∠AGC=
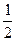 ×1200=600 ……………………….(3分)
×1200=600 ……………………….(3分)在Rt△ACG中,∠AGC= 600,AC=
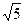
∴Sin600=
 ∴AG =
∴AG =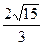 ……………………….(4分)
……………………….(4分)在Rt△AGH中, AH=OH-OA=a-1 ,GH=
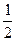 a+ 2
a+ 2 
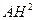 +
+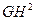 =
=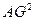
∴
 +
+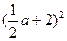 =
=
解之得:
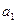 =
= ,
,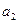 = ?
= ? (舍去) ……………………….(5分)
(舍去) ……………………….(5分) 点G的坐标为(
 ,
, + 2 ) ……………………….(6分) 解析:
+ 2 ) ……………………….(6分) 解析:略

练习册系列答案
相关题目
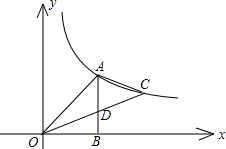 象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=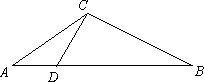
 (3)若点
(3)若点 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为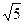 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.