题目内容
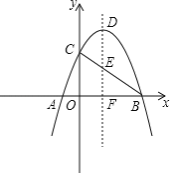
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+2mx+3m2与x轴相交于点B、C(点B在点C的左侧),与y轴相交于点A,点D为抛物线的顶点,抛物线的对称轴交x轴于点E.
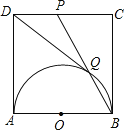
(1)如图1,当AO+BC=7时,求抛物线的解析式;
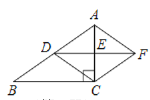
(2)如图2,点F是抛物线的对称轴右侧一点,连接BF、CF、DF,过点F作FH∥x轴交DE于点H,当∠BFC=∠DFB+∠BFH=90°时,求点H的纵坐标;
(3)如图3,在(1)的条件下,点P是抛物线上一点,点P、点A关于直线DE对称,点Q在线段AP上,过点P作PR⊥AP,连接BQ、QR,满足QB平分∠AQR,tan∠QRP=![]() ,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
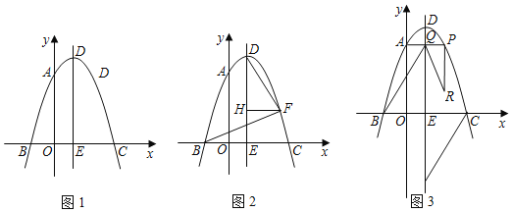
【答案】(1)y=﹣x2+2x+3;(2)1;(3)7
【解析】
(1)根据抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() ,可以求得
,可以求得![]() 的值,从而可以求得该抛物线的解析式;
的值,从而可以求得该抛物线的解析式;
(2)根据题意和三角形相似,作出合适的辅助线,可以求得点![]() 的纵坐标;
的纵坐标;
(3)根据在(1)的条件下,点![]() 是抛物线上一点,点
是抛物线上一点,点![]() 、点
、点![]() 关于直线
关于直线![]() 对称,点
对称,点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() ,连接
,连接![]() 、
、![]() ,满足
,满足![]() 平分
平分![]() ,
,![]() ,点
,点![]() 在抛物线的对称轴上且在
在抛物线的对称轴上且在![]() 轴下方,
轴下方,![]() ,利用勾股定理和三角形的全等可以求得线段
,利用勾股定理和三角形的全等可以求得线段![]() 的长.
的长.
解:(1)∵抛物线y=﹣x2+2mx+3m2=﹣(x﹣m)2+4m2=﹣(x﹣3m)(x+m),
∴当x=0时,y=3m2,当y=0时,x=3m或x=﹣m,该抛物线的顶点坐标为(m,4m2),
∵抛物线y=﹣x2+2mx+3m2与x轴相交于点B、C(点B在点C的左侧),与y轴相交于点A,点D为抛物线的顶点,
∴点A(0,3m2),点B(﹣m,0),点C(3m,0),点D(m,4m2),
∴AO=3m2,BC=4m,
∵AO+BC=7,
∴3m2+4m=7,
解得,m1=1,m2=﹣![]() (舍去),
(舍去),
∴抛物线的解析式为y=﹣x2+2x+3;
(2)连接EF,如图2所示,
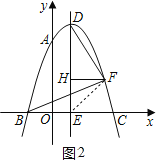
∵点B(﹣m,0),点C(3m,0),点D(m,4m2),点E是对称轴与x轴的交点,
∴BE=CE=2m,BC=4m,
∵∠BFC=90°,
∴EF=![]() BC=2m,
BC=2m,
∵HF∥x轴,
∴∠HFB=∠FBE,
∵EF=BE,
∴∠FBE=∠BFE,
∴∠HFB=∠BFE,
∵∠DFB+∠BFH=90°,
∴∠DFB+∠BFE=90°,
∴∠DFE=90°,
∵∠DFE=∠FHE=90°,∠DEF=∠FEH,
∴△DFE∽△FHE,
![]()
![]() ,
,
![]()
![]() ,
,
解得,EH=1,
∴点E的纵坐标为1;
(3)如图3,过点B作BM⊥PA交PA的延长线于点M,作BG⊥QR于点G,延长PR交x轴于点N,连接BR,
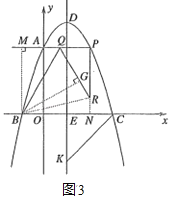
则四边形MBNP是矩形,
由(1)知点A(0,3),点D(1,4),点B(﹣1,0),点C(3,0),
∵点P与点A关于直线DE对称,
∴点P的坐标为(2,3),
∴点N(2,0)
∴BM=BN=3,
∴四边形MBNP是正方形,
∵QB平分∠AQR,
∴BM=BG,
∴BG=BN,
∵∠MQB=∠GQB,∠QMB=∠QGB=90°,QB=QB,
∴△MQB≌△GQB(AAS),
∴MQ=GQ,
同理可证,△BGR≌△BNR,
∴GR=NR,
∵tan∠QRP=![]() ,
,
∴设PQ=5k,则PR=12k,QR=13k,
∵MP=3,
∴MQ=3﹣5k,
∵NP=3,
∴RN=3﹣12k,
∵QR=QG+GR,MQ=GQ,GR=NR,
∴13k=3﹣5k+3﹣12k,
解得,k=![]() ,
,
∴PQ=1,MQ=2,
∵CE=BE=2,
∴CE=MQ,
∵CK=BQ,
∴Rt△BMQ≌Rt△KEC(HL),
∴BM=EK=3,
∴DK=DE+EK=4+3=7.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.
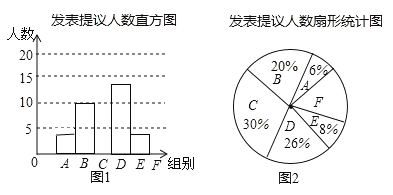
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取甲乙两所学校的名学生的数学成绩进行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据,分析数据:
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)经统计,表格中![]() 的值是__________.
的值是__________.
(2)得出结论
①若甲学校有600名初二学生,估计这次考试成绩80分以上人数为__________.
②可以推断出__________学校学生的数学水平较高,理由为:__________.(至少从两个不同的角度说明推断的合理性)