题目内容
11. 如图,梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.求证:AB=DC.
如图,梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.求证:AB=DC.
分析 根据SAS证明△ABM≌△DCM即可.
解答 证明:∵MA=MD,
∴∠MAD=∠MDA,
∵AD∥BC,
∴∠MAD=∠AMB,∠MDA=∠DMC,
∴∠AMB=∠DMC,
∵点M是BC的中点,
∴BM=CM,
在△ABM和△DMC中,
$\left\{\begin{array}{l}{MA=MD}\\{∠AMB=∠DMC}\\{BM=CM}\end{array}\right.$,
∴△ABM≌△DCM(SAS),
∴AB=DC.
点评 本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
3.下列方程中,是关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | 2x=1 | D. | ax2+bx+c=0 |
16.慧慧将方程2x2+4x-7=0通过配方转化为(x+n)2=p的形式,则p的值为( )
| A. | 7 | B. | 8 | C. | 3.5 | D. | 4.5 |
3.下列四个抛物线中,其对称轴和其他三个抛物线不相同的是( )
| A. | y=(x+2)2-8 | B. | y=(x+2)2-4 | C. | y=(x+2)2+8 | D. | y=(x-2)2-8 |
 为响应市委市政府提出的建设“绿色荆州”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)则小道进出口的宽度为1米.
为响应市委市政府提出的建设“绿色荆州”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)则小道进出口的宽度为1米.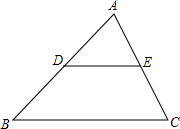 如图,在△ABC中,点D,E分别在边AB和AC上,且DE∥BC.
如图,在△ABC中,点D,E分别在边AB和AC上,且DE∥BC. (1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)
(1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)