题目内容
11．分解因式：（1）（x+2y）2-y2
（2）x2（x-y）+（y-x）
分析 （1）直接利用平方差公式分解因式得出即可；
（2）首先提取公因式（x-y），进而利用平方差公式分解因式得出即可．
解答 解：（1）（x+2y）2-y2
=（x+2y+y）（x+2y-y）
=（x+3y）（x-y）；
（2）x2（x-y）+（y-x）
=（x-y）（x2-1）
=（x-y）（x+1）（x-1）．
点评 此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
16．下列各式中正确的是（ ）
| A． | -（-2）＞-1 | B． | |-0.2|=-0.2 | C． | |-5|＜0 | D． | -$\frac{3}{2}$＞-$\frac{1}{2}$ |
20．先阅读下列一段文字，然后解答问题：
某运输部门规定：办理托运，当一种物品的重量不超过16千克时，需付基础费30元和保险费a元：为限制过重物品的托运，当一件物品超过16千克时，除了付以上基础费和保险费外，超过部分每千克还需付b元超重费．设某件物品的重量为x千克．
（1）当x≤16时，支付费用为a+30元（用含a的代数式表示）；当x≥16时，支付费用为a+30+（x-16）b元（用含x和a、b的代数式表示）；
（2）甲、乙两人各托运一件物晶，物品重量和支付费用如下表所示
①试根据以上提供的信息确定a，b的值．
②试问在物品可拆分的情况下，用不超过105元的费用能否托运50千克物品？若能，请设计出其中一种托运方案，并求出托运费用；若不能，请说明理由．
某运输部门规定：办理托运，当一种物品的重量不超过16千克时，需付基础费30元和保险费a元：为限制过重物品的托运，当一件物品超过16千克时，除了付以上基础费和保险费外，超过部分每千克还需付b元超重费．设某件物品的重量为x千克．
（1）当x≤16时，支付费用为a+30元（用含a的代数式表示）；当x≥16时，支付费用为a+30+（x-16）b元（用含x和a、b的代数式表示）；
（2）甲、乙两人各托运一件物晶，物品重量和支付费用如下表所示
| 物品重量（千克） | 支付费用（元） |
| 18 | 38 |
| 25 | 53 |
②试问在物品可拆分的情况下，用不超过105元的费用能否托运50千克物品？若能，请设计出其中一种托运方案，并求出托运费用；若不能，请说明理由．
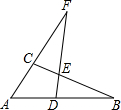如图，△ABC中，D，E分别是AB和BC上的点，直线DE与AC的延长线交于点F，且AD•AB=AC•AF．求证：