题目内容
3.若横断面直径为1米的圆形下水管道的水面宽为0.8米,则下水管道中最深处的水深为0.2米或0.8米.分析 分为两种情况,画出图形,先连接OA,过O作OC⊥AB于点D,由垂径定理可知AD=$\frac{1}{2}$AB,再在Rt△OAD中利用勾股定理可求出OD的长,再根据CD=OC-OD或CD=OC+OD即可得出结论.
解答  解:分为两种情况:
解:分为两种情况:
①如图1所示:连接OA,过O作OC⊥AB于点D,
∵OC⊥AB,AB=0.8米.
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×0.8=0.4米,
∵圆形污水管道的直径为1米,
∴OA=OC=0.5米,
在Rt△OAD中,OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=0.3(米),
∴CD=OC-OD=0.5-0.3=0.2(米).
②如图2所示:CD=0.5+0.3=0.8(米),
故答案为:0.2米或0.8米.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
18.下列事件是随机事件的是( )
| A. | 在标准大气压下,水加热到100°时沸腾 | |
| B. | 小明购买1张彩票,中奖 | |
| C. | 在一个装有红球和黄球的袋中,摸出蓝球 | |
| D. | 一名运动员的速度为30米/秒 |
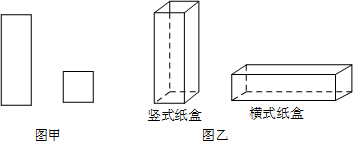
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |

12. 如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
 如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )| A. | 30° | B. | 25° | C. | 20° | D. | 15° |
13.下列命题中,属于真命题的是( )
| A. | 两个锐角的和是锐角 | B. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c | ||
| C. | 同位角相等 | D. | 在同一平面内,如果a∥b,b∥c,则a∥c |
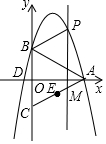 如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(-1,0),点C与点B关于x轴对称,连接AB、AC.
如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(-1,0),点C与点B关于x轴对称,连接AB、AC.