题目内容
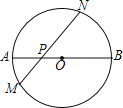
【题目】已知二次函数![]() 的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的个数是( )
的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的个数是( )
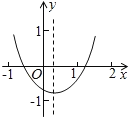
A.1B.2C.3D.4
【答案】B
【解析】
①据当x=1时图象在x轴下方,得出y<0,即a+b+c<0判断即可;
②据当x=-1时图象在x轴上方,得出y>0,即a-b+c>0判断即可;
③据对称轴![]() <1,得出2a+b>0进行判断;
<1,得出2a+b>0进行判断;
④由图象开口向上判断出a>0,由对称轴在y轴右侧得出b<0,由抛物线与y轴交于负半轴,c<0判断即可.
解:①当x=1时图象在x轴下方时,y<0,
即a+b+c<0,①正确;
②当x=-1时图象在x轴上方,y>0,
即a-b+c>0,②错误;
③由抛物线的开口向上知a>0,
∵![]() <1,
<1,
∴2a+b>0,③错误;
④∵图象开口向上,
∴a>0,
∵对称轴在y轴右侧
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,④正确,
∴正确的结论有2个;
故选:B.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某中学共有学生2000名,各年级男、女生人数如下表:
年级 | 六年级 | 七年级 | 八年级 | 九年级 |
男生 | 250 | z | 254 | 258 |
女生 | x | 244 | y | 252 |
若从全校学生中任意抽取一名,抽到六年级女生的概率是0.12;若将各年级的男、女学生人数制成扇形统计图,八年级女生对应扇形的圆心角为44.28°.
(1)求x,y,z的值;
(2)求各年级女生的平均数;
(3)如果从八年级随机抽取36名学生参加社会实践活动,求抽到八年级某同学的概率.