Question

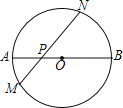
【题目】如图，在⊙O中，直径AB与弦MN相交于点P，∠NPB＝45°，若AP＝2，BP＝6，则MN的长为（ ）

A.B.2C.2D.8

Answer 1

【答案】C

【解析】

过点O作OD⊥MN于点D，连接ON，先根据AB是直径，AP=2，BP=6求出⊙O的半径，故可得出OP的长，因为∠NPB=45°，所以△OPD是等腰直角三角形，再根据勾股定理求出OD的长，故可得出DN的长，由此即可得出结论．

解：过点O作OD⊥MN于点D，连接ON，则MN＝2DN，

∵AB是⊙O的直径，AP＝2，BP＝6，

∴⊙O的半径＝×（2+6）＝4，

∴OP＝4﹣AP＝4﹣2＝2，

∵∠NPB＝45°，

∴△OPD是等腰直角三角形，

∴OD＝，

在Rt△ODN中，

DN＝，

∴MN＝2DN＝2．

故答案为：C．