题目内容
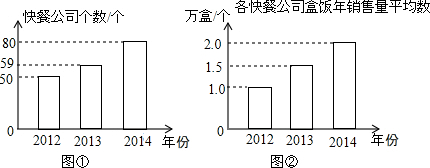
5. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32).
分析 由直线解析式可求得A1,然后分别求得B1,B2,B3…的坐标,可以得到规律:Bn(2n-1,2n-1),据此即可求解.
解答 解:
∵直线解析式是:y=x+1,
∴OA1=1
∴A1B1=1,
∴C1坐标为(1,0),
∴A2坐标为(1,2),
∴点B2的坐标为(3,2),
∴点A3的坐标为(3,4),
∴A3C2=A3B3=B3C3=4,
∴点B3的坐标为(7,4),
∴B1的纵坐标是:1=20,B1的横坐标是:1=21-1,
∴B2的纵坐标是:2=21,B2的横坐标是:3=22-1,
∴B3的纵坐标是:4=22,B3的横坐标是:7=23-1,
∴Bn的纵坐标是:2n-1,横坐标是:2n-1,
则Bn(2n-1,2n-1).
∴B6的坐标是:(26-1,26-1),即(63,32).
故答案为:(63,32).
点评 此题主要考查了待定系数法求函数解析式和坐标的变化规律.此题难度较大,注意正确得到点的坐标的规律是解题的关键

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.把多项式4a3-8a2b+4ab2分解因式,结果正确的是( )
| A. | a(2a+b)(a-2b) | B. | 4a(a2-2ab+b2) | C. | a(2a-b)2 | D. | 4a(a-b)2 |
16. 如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )
如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )
 如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )
如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
10.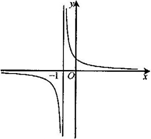 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
经验:
(1)我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的:
①由数想到形----先根据表达式中x、y的数量关系,初步估计图象的基本概貌.如:形状(直线或曲线);位置(所在区域、与直线或坐标轴的交点情况);趋势(上升、下降);对称性等.
②描点画图----根据已有的函数画图的经验,利用描点画图.
(2)我们知道,函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线,一支在过点(-1,0)且平行于y轴的直线的右侧且在x轴的上方,另一支在过点(-1,0)且平行于y轴的直线的左侧且在x轴的下方.
探索:请你根据以上经验,研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题.
(1)由数想形:
(2)描点画图:
①列表:
②画图:
应用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0;
(4)直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围.
 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?经验:
(1)我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的:
①由数想到形----先根据表达式中x、y的数量关系,初步估计图象的基本概貌.如:形状(直线或曲线);位置(所在区域、与直线或坐标轴的交点情况);趋势(上升、下降);对称性等.
②描点画图----根据已有的函数画图的经验,利用描点画图.
(2)我们知道,函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线,一支在过点(-1,0)且平行于y轴的直线的右侧且在x轴的上方,另一支在过点(-1,0)且平行于y轴的直线的左侧且在x轴的下方.
探索:请你根据以上经验,研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题.
(1)由数想形:
(2)描点画图:
①列表:
| x | … | … | |||||||||||||||
| y | … | … |

应用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0;
(4)直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围.
15. 如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
 如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )| A. | 25° | B. | 30° | C. | 50° | D. | 60° |
 如图,方格子的边长为1,△ABC的顶点在格点上.
如图,方格子的边长为1,△ABC的顶点在格点上. 如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.
如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.