题目内容
5.求满足下列条件的二次函数的表达式:(1)已知抛物线y=ax2+bx+c经过三点(0,-2),(1,0),(2,3);
(2)已知抛物线y=ax2+bx+c经过三点(0,-1),(1,2),(-1,0);
(3)已知抛物线y=ax2+bx+c经过三点(-1,2),(0,1),(2,-7).
分析 (1)将三点代入,列出三元一次方程组,求解即可;
(2)将三点代入,列出三元一次方程组,求解即可;
(3)将三点代入,列出三元一次方程组,求解即可.
解答 解:(1)将三点(0,-2),(1,0),(2,3)代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{c=-2}\\{a+b+c=0}\\{4a+2b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{3}{2}}\\{c=-2}\end{array}\right.$,
∴二次函数的表达式为y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2;
(2)将三点(0,-1),(1,2),(-1,0)代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{a-b+c=0}\\{a+b+c=2}\\{c=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=-1}\end{array}\right.$,
∴二次函数的表达式为y=2x2+x-1;
(3)将三点(-1,2),(0,1),(2,-7)代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{a-b+c=2}\\{c=1}\\{4a+2b+c=-7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=1}\end{array}\right.$,
∴二次函数的表达式为y=-x2-2x+1.
点评 本题考查了用待定系数法求二次函数的解析式,掌握三元一次方程组的解法是解题的关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案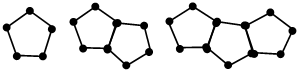 用火柴棒按如图的方式搭五边形组成的图形
用火柴棒按如图的方式搭五边形组成的图形(1)填写表:
| 五边形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
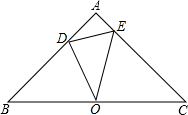 如图,△ABC是等腰直角三角形,∠A=90°,O是BC的中点,点D和点E分别在AB、AC上,∠DOE=45°.
如图,△ABC是等腰直角三角形,∠A=90°,O是BC的中点,点D和点E分别在AB、AC上,∠DOE=45°.