��Ŀ����
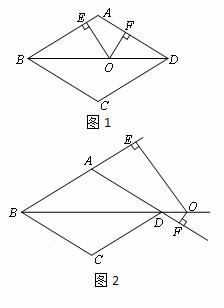
��ͼ���ڱ߳�Ϊ10������ABCD�У��Խ���BD��16����O��ֱ��BD�ϵĶ��㣬OE��AB��E��OF��AD��F��
��1���Խ���AC�ij��� ������ABCD������� ��
��2����ͼ1������O�ڶԽ���BD���˶�ʱ��OE��OF��ֵ�Ƿ����仯����˵�����ɣ�
��3����ͼ2������O�ڶԽ���BD���ӳ�����ʱ��OE��OF��ֵ�Ƿ����仯�������䣬��˵�����ɣ����仯����̽��OE��OF֮���������ϵ����˵�����ɣ�
��1��12��96 ��
��2��OE+OF=9��6�Ƕ�ֵ�����䣻
��3��OE+OF��ֵ�仯��OE��OF֮���������ϵΪ��OE-OF=9��6
��������
��������1������AC��BD�ཻ�ڵ�G���������εĶԽ����ഹֱƽ�����BG�������ù��ɶ�����ʽ���AG��Ȼ�����AC=2AG���㼴�ɵý⣻�ٸ������ε�������ڶԽ��߳˻���һ����ʽ���㼴�ɵý⣻
��2������AO������S��ABD=S��ABO+S��ADO��ʽ���㼴�ɵý⣻
��3������AO������S��ABD=S��ABO-S��ADO��ʽ�������ɵý⣮
�⣺��1����ͼ������AC��BD�ཻ�ڵ�G��

������ABCD��AC��BD��BG= BD=
BD= ��16=8��
��16=8��
�ɹ��ɶ����ã�AG= =6��
=6��
��AC=2AG=2��6=12��
����ABCD�����= AC•BD=
AC•BD= ��12��16=96��
��12��16=96��
�ʴ�Ϊ��12��96��
��2����ͼ������AO��

��
���ԣ� BD•AG=
BD•AG= AB•OE+
AB•OE+ AD•OF��
AD•OF��
�� ��16��6=
��16��6= ��10•OE+
��10•OE+ ��10•OF��
��10•OF��
���OE+OF=9��6�Ƕ�ֵ�����䣻
��3����ͼ������AO��

��
���ԣ� BD•AG=
BD•AG= AB•OE-
AB•OE- AD•OF��
AD•OF��
�� ��16��6=
��16��6= ��10•OE-
��10•OE- ��10•OF��
��10•OF��
���OE-OF=9��6���Ƕ�ֵ�����䣬
���ԣ�OE+OF��ֵ�仯��OE��OF֮���������ϵΪ��OE-OF=9��6��
���Ѷȡ�����

 �У��Ա���
�У��Ա��� ��ȡֵ��Χ�� .
��ȡֵ��Χ�� . ��ͼ��Ľ��㣮
��ͼ��Ľ��㣮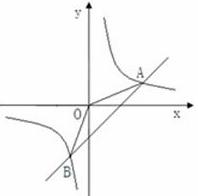

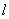 ��
��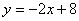 �ֱ���
�ֱ���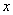 �ᡢ
�ᡢ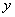 �ύ��A��B���㣬��C�߶�AB�ϣ���CD��x����D, CD=2OD, ��E�߶�OB��,��AE=BE��
�ύ��A��B���㣬��C�߶�AB�ϣ���CD��x����D, CD=2OD, ��E�߶�OB��,��AE=BE��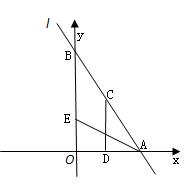
 ����E���ҽ���AOB�ֳ������Ϊ1��2�������֣���ֱ��
����E���ҽ���AOB�ֳ������Ϊ1��2�������֣���ֱ��