题目内容
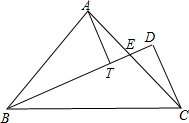 如图,在等腰△ABC中,AB=AC,∠BAC=90°,BE平分∠BAC交AC于E,过C作CD⊥BE于D,过A点作AT⊥FD,写出BD-CD与AT之间的数量关系并证明.
如图,在等腰△ABC中,AB=AC,∠BAC=90°,BE平分∠BAC交AC于E,过C作CD⊥BE于D,过A点作AT⊥FD,写出BD-CD与AT之间的数量关系并证明.考点:全等三角形的判定与性质
专题:
分析:在BD上截取BF=CD,连接AD,求出∠ACD=∠ABF,求出三角形ABF和三角形ACD全等,推出AF=AD,求出三角形FAD是等腰直角三角形,即可得出答案.
解答:答:AT=
(BD-CD),
证明:在BD上截取BF=CD,连接AD,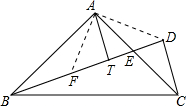
∵CD⊥BD,
∴∠CDE=∠BAE=90°,
∵∠AEB=∠DEC,∠ABF+∠AEB+∠BAE=180°,∠DCE+∠DEC+∠CDE=180°,
∴∠ABF=∠DCE,
在△ABF和△ACD中,
,
∴△ABF≌△ACD(SAS),
∴AF=AD,∠BAF=∠DAC,
∵∠BAC=∠BAF+∠FAC=90°,
∴∠DAC+∠FAE=∠FAD=90°,
即△FAD是等腰直角三角形,
∵AT⊥DF,
∴FT=TD,
∴AT=
DF=
(BD-CD).
| 1 |
| 2 |
证明:在BD上截取BF=CD,连接AD,

∵CD⊥BD,
∴∠CDE=∠BAE=90°,
∵∠AEB=∠DEC,∠ABF+∠AEB+∠BAE=180°,∠DCE+∠DEC+∠CDE=180°,
∴∠ABF=∠DCE,
在△ABF和△ACD中,
|
∴△ABF≌△ACD(SAS),
∴AF=AD,∠BAF=∠DAC,
∵∠BAC=∠BAF+∠FAC=90°,
∴∠DAC+∠FAE=∠FAD=90°,
即△FAD是等腰直角三角形,
∵AT⊥DF,
∴FT=TD,
∴AT=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等腰直角三角形性质,全等三角形的性质和判定的应用,解此题的关键是求出三角形FAD是等腰直角三角形,题目比较好,有一定的难度.

练习册系列答案
相关题目
 正方形的网格中,每个小正方形的边长为1,则网格中三角形ABC中,边长是无理数的边数是( )
正方形的网格中,每个小正方形的边长为1,则网格中三角形ABC中,边长是无理数的边数是( )| A、0 | B、1 | C、2 | D、3 |
 两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01).
两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01).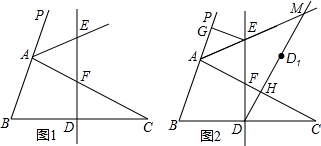
 如图,菱形ABCD的边长是2cm,E是AB中点,且DE⊥AB,则DE的长为
如图,菱形ABCD的边长是2cm,E是AB中点,且DE⊥AB,则DE的长为