题目内容
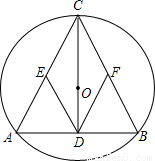
 如图,圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,若图中3个阴影三角形的面积之和为4,内切圆半径为1,则△ABC的周长为
如图,圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,若图中3个阴影三角形的面积之和为4,内切圆半径为1,则△ABC的周长为
- A.4
- B.8
- C.12
- D.16
D
分析:根据图中3个阴影三角形的面积之和为4,得出△ABC的面积为:8,进而利用 ×1×△ABC的周长=8求出答案即可.
×1×△ABC的周长=8求出答案即可.
解答:∵圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,图中3个阴影三角形的面积之和为4,
∴△ABC的面积为:8,
∵内切圆半径为1,
∴ ×1×△ABC的周长=8,
×1×△ABC的周长=8,
则△ABC的周长为:16.
故选:D.
点评:此题主要考查了三角形的内切圆与内心,根据三角形内切圆半径乘以三角形周长除以2得出三角形面积是解题关键.
分析:根据图中3个阴影三角形的面积之和为4,得出△ABC的面积为:8,进而利用
 ×1×△ABC的周长=8求出答案即可.
×1×△ABC的周长=8求出答案即可.解答:∵圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,图中3个阴影三角形的面积之和为4,
∴△ABC的面积为:8,
∵内切圆半径为1,
∴
 ×1×△ABC的周长=8,
×1×△ABC的周长=8,则△ABC的周长为:16.
故选:D.
点评:此题主要考查了三角形的内切圆与内心,根据三角形内切圆半径乘以三角形周长除以2得出三角形面积是解题关键.

练习册系列答案
相关题目
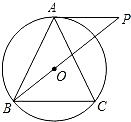 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P. 已知:如图,圆O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点,求证:四边形CEDF是菱形.
已知:如图,圆O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点,求证:四边形CEDF是菱形. (2012•衡水一模)如图,圆O是△ABC的外接圆,连接OB、OC,圆O的半径R=10,sinA=
(2012•衡水一模)如图,圆O是△ABC的外接圆,连接OB、OC,圆O的半径R=10,sinA=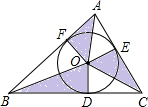 如图,圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,若图中3个阴影三角形的面积之和为4,内切圆半径为1,则△ABC的周长为( )
如图,圆O是△ABC的内切圆,与△ABC各边的切点分别为D、E、F,若图中3个阴影三角形的面积之和为4,内切圆半径为1,则△ABC的周长为( )