题目内容
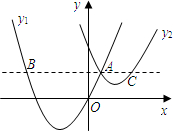 如图,抛物线y1=a(x+2)2+c与y2=
如图,抛物线y1=a(x+2)2+c与y2=| 1 |
| 2 |
| A、c=4a |
| B、a=1 |
| C、当x=0时,y2-y1=4 |
| D、2AB=3AC |
考点:二次函数的性质
专题:
分析:把点A坐标与原点坐标代入y1,求出a、c的值,即可得到函数解析式,把点A坐标代入y2,求出b的值,即可得到函数解析式,判定A、B错误;令x=0,求出y2与y轴的交点,判定C错误;令y=3,求出A、B、C的横坐标,然后求出AB、AC的长,判定D正确.
解答:解:∵y1=a(x+2)2+c经过点A(1,3)与原点,
∴
,
解得
,
∴c=-4a,故A、B选项错误;
y1=
(x+2)2-
,
∵y2=
(x-3)2+b经过点A(1,3),
∴
(1-3)2+b=3,
解得b=1,
∴y2=
(x-3)2+1,
当x=0时,y=
(0-3)2+1=5.5,
此时y2-y1=5.5,故C选项错误;
∵过点A作x轴的平行线,分别交两条抛物线于点B,C,
∴令y=3,则
(x+2)2-
=3,
整理得,(x+2)2=9,
解得x1=-5,x2=1,
∴AB=1-(-5)=6,
(x-3)2+1=3,
整理得,(x-3)2=4,
解得x1=5,x2=1,
∴AC=5-1=4,
∴2AB=3AC,故D选项正确.
故选D.
∴
|
解得
|
∴c=-4a,故A、B选项错误;
y1=
| 3 |
| 5 |
| 12 |
| 5 |
∵y2=
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得b=1,
∴y2=
| 1 |
| 2 |
当x=0时,y=
| 1 |
| 2 |
此时y2-y1=5.5,故C选项错误;
∵过点A作x轴的平行线,分别交两条抛物线于点B,C,
∴令y=3,则
| 3 |
| 5 |
| 12 |
| 5 |
整理得,(x+2)2=9,
解得x1=-5,x2=1,
∴AB=1-(-5)=6,
| 1 |
| 2 |
整理得,(x-3)2=4,
解得x1=5,x2=1,
∴AC=5-1=4,
∴2AB=3AC,故D选项正确.
故选D.
点评:本题考查了二次函数的性质,主要利用了待定系数法求二次函数解析式,已知函数值求自变量的值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
下列计算正确的是( )
| A、a+a=a2 |
| B、a3•a5=a8 |
| C、(a3)4=a7 |
| D、(-a-b)(b-a)=b2-a2 |
如图,已知AB=AC,AB∥EF,若∠CDE=60°,则∠C等于( )

| A、15° | B、30° |
| C、45° | D、60° |
当m为何值时,方程
=
产生增根( )
| x-1 |
| x-3 |
| m |
| x-3 |
| A、2 | B、3 | C、4 | D、5 |
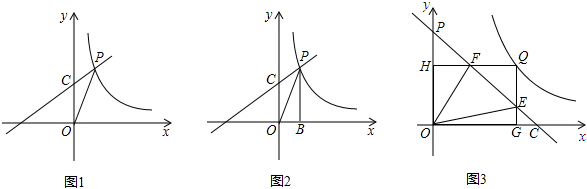
 如图,已知直线l:y=kx+b与直线m:y=mx+n相交于点P (-3,-2),则关于x的不等式mx+n<kx+b的解为
如图,已知直线l:y=kx+b与直线m:y=mx+n相交于点P (-3,-2),则关于x的不等式mx+n<kx+b的解为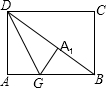 如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )
如图,在矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,点A落在点A1处,则AG的长为( )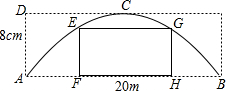 有一个抛物线形拱桥,其最大高度AD为8m,跨度AB为20m,为了对拱桥进行加固,需要在拱桥内安装矩形脚手架EFHG,已知脚手架的高EF为5m.
有一个抛物线形拱桥,其最大高度AD为8m,跨度AB为20m,为了对拱桥进行加固,需要在拱桥内安装矩形脚手架EFHG,已知脚手架的高EF为5m.