Question

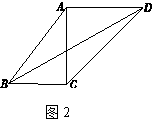
【题目】如图，在四边形ABCD中，AD//BC ， AB=10，BC=6，AC=AD=8．

（1）求∠ACB的度数；
（2）求CD边的长.

Answer 1

【答案】
（1）

解：如图2．

∵ △ABC中，AB=10，BC=6，AC =8，

∴ .

∴ △ABC是直角三角形，

（2）

解：∵ AD//BC，

∴ .

∵ 在Rt△ACD中， ，AC=AD=8，

∴

【解析】（1） △ABC中，由已知条件根据勾股定理逆定理得出AC2+BC2=AB2 ;从而得到 ∠ACB=90°.
（2）由 AD//BC，得到∠CAD=∠ACB=90° ；在Rt△ACD中，再根据勾股定理得到 CD2=AC2+AD2 ， 从而求出CD的长度.
【考点精析】关于本题考查的平行线的性质和勾股定理的概念，需要了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．