题目内容
10.观察下列各等式:$\frac{1}{1×2}=\frac{1}{2}=\frac{1}{1}-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{6}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{12}=\frac{1}{3}-\frac{1}{4}$…根据你发现的规律,计算:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2012×2013}$+$\frac{1}{2013×2014}$:
(2)$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{n(n+1)}$.(n为正整数)
分析 (1)原式利用拆项法变形,计算即可得到结果;
(2)原式提取2,再利用拆项法变形,计算即可得到结果.
解答 解:(1)根据题意得:原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$=1-$\frac{1}{2014}$=$\frac{2013}{2014}$;
(2)原式=2($\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{n(n+1)}$)=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.计算$\sqrt{2}$($\sqrt{6}$÷$\sqrt{3}$)的结果是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
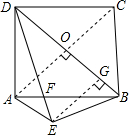 正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE.
正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE. 如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE.
如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE.