题目内容
7、一元二次方程ax2+bx+c=0（a≠0）中，若a，b都是偶数，c是奇数，则这个方程（ ）
分析：利用已知条件假设出一根，代入方程，根据所得结果的奇偶性，可以排除A，再利用特殊值法可求出B，C不正确，从而确定答案．
解答：解：假设有整数根，不妨设它的根是2k或2k+1（k为整数），分别代入原方程得，
方程两边的奇偶性不同的矛盾结果，所以排除A；若a，b，c分别取4，8，3则排除C，D．
故选B．
方程两边的奇偶性不同的矛盾结果，所以排除A；若a，b，c分别取4，8，3则排除C，D．
故选B．
点评：此题主要考查了一元二次方程根整数根的有关知识，以及整数的奇偶性，难度不大，题目比较典型．
练习册系列答案
相关题目
一元二次方程ax2+bx+c=0（a≠0，b2-4ac≥0）的两实根之和（ ）
| A、与c无关 | B、与b无关 | C、与a无关 | D、与a，b，c都有关 |
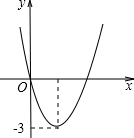（2012•泰安）二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）