题目内容
若x1、x2为一元二次方程ax2+bx+c=0（a≠0）的两根，则有x1+x2=-
，x1•x2=
，根据材料回答问题：若x1、x2是一元二次方程2x2-4x+1=0的两根，则（x1+1）（x2+1）=
．
| b |
| a |
| c |
| a |
| 7 |
| 2 |
| 7 |
| 2 |
分析：根据根与系数的关系得到x1+x2=-
=2，x1•x2=
，再把（x1+1）（x2+1）去括号整理得到x1•x2+x1+x2+1，然后利用整体思想进行计算．
| -4 |
| 2 |
| 1 |
| 2 |
解答：解：根据题意得x1+x2=-
=2，x1•x2=
，
（x1+1）（x2+1）
=x1•x2+x1+x2+1
=
+2+1
=
．
故答案为
．
| -4 |
| 2 |
| 1 |
| 2 |
（x1+1）（x2+1）
=x1•x2+x1+x2+1
=
| 1 |
| 2 |
=
| 7 |
| 2 |
故答案为
| 7 |
| 2 |
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-
，x1•x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
相关题目
（2012•兰州）若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-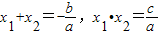
．我们把它们称为根与系数关系定理．
=
=
=
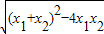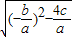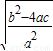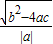
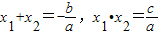．我们把它们称为根与系数关系定理．
=
=
=
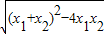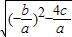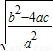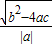
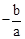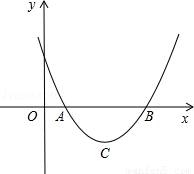
，x1•x2＝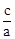
．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝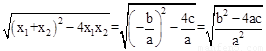
。
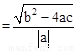