Question

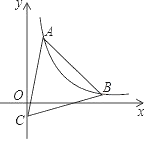
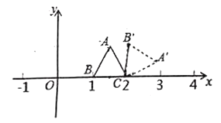
【题目】如图，在平面直角坐标系中，正方形顶点为轴正半轴上一点，点在第一象限，点的坐标为，连接.动点在射线上（点不与点、点重合），点在线段的延长线上，连接、，，设的长为.

（1）填空：线段的长=________，线段的长=________；

（2）求的长，并用含的代数式表示.

Answer 1

【答案】（1）（1）4，；（2）或

【解析】

（1）根据点的横坐标可得OA的长，根据勾股定理即可求出OB的长；

（2）①点在轴正半轴,可证≌，得到，从而求得；

②点在轴负半轴,过点做平行轴的直线,分别交轴、的延长线于点、，证得≌，．

解：（1）∵B（4，4），∴OA=4，AB=4，∵∠OAB=90°，∴．

故答案为：4；；

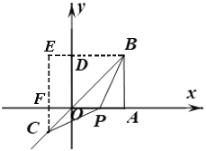
（2）①点在轴正半轴，过点做平行轴的直线，分别交轴、的延长线于点、．

∵，，∴．

同理．

∴，，

∵轴，∴．

∴，∴，

∵，∴．

∴．

∴≌．

∴，

∴．

∴；

②点在轴负半轴，过点做平行轴的直线，分别交轴、的延长线于点、．

∵,，∴，

同理．

∴，．

∵轴，∴．

∴，∴．

∵，∴．

∴．

∴≌．

∴，

∴．

∴；

∴或．