题目内容
一个四位数是奇数,它的首位数字小于其余各位数码,而百位数大于其余各位数码,其十位数等于首末两位数码和的两倍,求这个四位数.
考点:整数问题的综合运用
专题:常规题型
分析:由题意可知,这个四位数为奇数,则其个数为1、3、5、7、9中的一个数.又十位数字等于首末两位数字的和的两倍,所以十位数字最大可为8,而首末两位数字的和不能大于4.而首位数字小个位数字,所以首位数字只能为1,个位数只能为3.则十位数字为(1+3)×2=8.又第二位数字大于其他各位数字,所以第二位数字为9.则这个数为1983.
解答:解:由于个四位数为奇数,则其个数为1、3、5、7、9中的一个数;
又十位数字等于首末两位数字的和的两倍,
所以首末两位数字的和不能大于4;
而首位数字<个位数字,
所以首位数字只能为1,个位数只能为3;
则十位数字为(1+3)×2=8.
又百位数字大于其他各位数字,
所以百位数字为9.
综上所述,这个数为:1983.
又十位数字等于首末两位数字的和的两倍,
所以首末两位数字的和不能大于4;
而首位数字<个位数字,
所以首位数字只能为1,个位数只能为3;
则十位数字为(1+3)×2=8.
又百位数字大于其他各位数字,
所以百位数字为9.
综上所述,这个数为:1983.
点评:本题主要考查整数问题的综合运用的知识点,首先根据已知条件确定这个数的首末两位数字是几是完成本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ?ABCD中,E是BC的中点,AE=9,BD=12,AD=10,则△ABD的面积为( )
?ABCD中,E是BC的中点,AE=9,BD=12,AD=10,则△ABD的面积为( )| A、24 | B、30 | C、36 | D、40 |
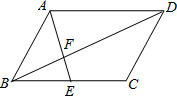
 已知△ABC中,AD与BE交于点F,且AE:EC=3:2,BD:BC=1:3,求S△ABF:S四边形DCEF.
已知△ABC中,AD与BE交于点F,且AE:EC=3:2,BD:BC=1:3,求S△ABF:S四边形DCEF. 如图在抛物线y=x(a-x)(a>0)与x轴所围图形的内接矩形ABCD(边BC在x轴上)中,当矩形周长最大时,它的两边长AB=
如图在抛物线y=x(a-x)(a>0)与x轴所围图形的内接矩形ABCD(边BC在x轴上)中,当矩形周长最大时,它的两边长AB= 如图ABCD是正方形,标出的其余各点都是所在边的三等分点.试问图中有多少个矩形(包括正方形)?
如图ABCD是正方形,标出的其余各点都是所在边的三等分点.试问图中有多少个矩形(包括正方形)?