题目内容
14.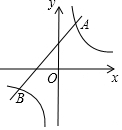 如图,已知点A(2,a),B(-4,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知点A(2,a),B(-4,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)观察图象,求关于x的不等式kx+b≤$\frac{m}{x}$的解.
分析 (1)先把B点坐标代入y=$\frac{m}{x}$求出m得到反比例函数解析式为y=$\frac{8}{x}$,再利用反比例函数解析式求出a,则可确定A点坐标,然后利用待定系数法求一次函数解析式;
(2)利用函数图象,写出反比例函数图象不在一次函数图象下方所对应的自变量的范围即可.
解答 解:(1)把B(-4,-2)代入y=$\frac{m}{x}$得m=-4×(-2)=8,
所以反比例函数解析式为y=$\frac{8}{x}$,
把A(2,a)代入y=$\frac{8}{x}$得2a=8,解得a=4,
把A(2,4),B(-4,-2)代入y=kx+b得$\left\{\begin{array}{l}{2k+b=4}\\{-4k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
所以一次函数解析式为y=x+2;
(2)当x≤-4或0<x≤2时,x+2≤$\frac{8}{x}$,
所以关于x的不等式kx+b≤$\frac{m}{x}$的解集为x≤-4或0<x≤2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
5.已知反比例函数y=$\frac{6}{x}$,在下列结论中,错误的是( )
| A. | 图象位于第一、三象限 | B. | 图象必经过点(-2,-3) | ||
| C. | y随x的增大而增大 | D. | 若x>2,则y<3 |
9.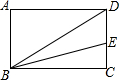 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 3 | D. | 4 |
19.若x=1是方程2x+m-6=0的解,则m的值是( )
| A. | 4 | B. | -4 | C. | -8 | D. | 8 |
7.一个两位数的两个数字之和为11,两个数字之差为5.求这个两位数,此题的解( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
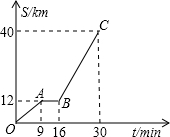 如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题: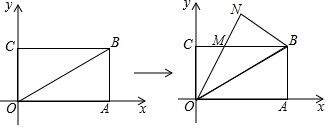

 尺规作图
尺规作图