题目内容
8. 如图,四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AB=5,BD=6$\sqrt{2}$,则边BC的长为( )
如图,四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AB=5,BD=6$\sqrt{2}$,则边BC的长为( )| A. | 5$\sqrt{2}$ | B. | 6 | C. | 7 | D. | 6$\sqrt{2}$ |
分析 延长BC到E,使CE=AB,连接DE,易证∠BAD=∠DCE,即可证明△DAB≌△DCE,可得∠ADB=∠CDE,BD=DE=6$\sqrt{2}$,CE=AB=5,即可求证△BDE为等腰直角三角形,即可求得BE的长,进而即可求得BC=BE-CE=12-5=7.
解答  解:延长BC到E,使CE=AB,连接DE,
解:延长BC到E,使CE=AB,连接DE,
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠BAD=∠DCE,
∵在△DAB和△DCE中,
$\left\{\begin{array}{l}{AB=CE}\\{∠BAD=∠DCE}\\{AD=DC}\end{array}\right.$,
∴△DAB≌△DCE,(SAS)
∴∠ADB=∠CDE,BD=DE=6$\sqrt{2}$,CE=AB=5,
∵∠ADB+∠BDC=∠ADC=90°,
∴∠BDE=∠CDE+∠BDC=90°,
∴△BDE为等腰直角三角形,
∴BE=$\sqrt{2}$BD=12,
∴BC=BE-CE=12-5=7.
故选C.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△DAB≌△DCE是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.观察下列各单项式:a,-2a2,4a3,-8a4,16a5,-32a6,…,根据你发现的规律,第10个单项式是( )
| A. | -29a10 | B. | 29a10 | C. | 210a10 | D. | -210a10 |
 如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.
如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$. 如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=20,AC=32.点P从点A出发,以每秒4个单位的速度沿线段AC向点C运动,同时,点Q从点O出发,以每秒3个单位的速度沿折线OD-DC向点C运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接BP、PQ、BQ,设点Q的运动时间为t秒.
如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=20,AC=32.点P从点A出发,以每秒4个单位的速度沿线段AC向点C运动,同时,点Q从点O出发,以每秒3个单位的速度沿折线OD-DC向点C运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接BP、PQ、BQ,设点Q的运动时间为t秒.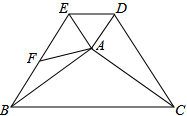 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为2$\sqrt{7}$.
新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为2$\sqrt{7}$.