Question

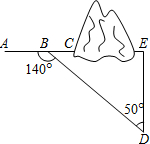如图，在某隧道建设工程中，需沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工．为了使开挖点E在直线AC上，现在AC上取一点B，AC外取一点D，测得∠ABD=140°，BD=704m，∠D=50°．求开挖点E到点D的距离．
（精确到1米） 参考数据：sin50°=0.8，cos50°=0.6，tan50°=1.2．

Answer 1

考点：解直角三角形的应用

专题：

分析：先根据∠ABD=140°，∠D=50°，求出∠E=90°，判断出△BED为直角三角形，再根据锐角三角函数的定义进行求解即可．

解答：解：根据题意得：BD=704m，∠ABD=140°，∠D=50°．
∵∠EBD=180°-∠ABD，
∴∠EBD=180°-140°=40°．
在△BDE中，∠E=180°-∠EBD-∠D，
∴∠E=180°-40°-50°=90°，
∴△BED为直角三角形，
在Rt△BED中，
∵cos∠D=

DE

BD

，
∴DE=BD×cos50°=704×0.6=422.4≈422（m）．
答：开挖点E到点D的距离为422m．

点评：本题考查的是解直角三角形在实际生活中的运用，涉及到三角形内角和定理及锐角三角函数的定义，熟知以上知识是解答此题的关键．