题目内容
 已知反比例函数y=
已知反比例函数y=| 12k |
| x |
| y2-y1 |
| x2-x1 |
| 1 |
| 2 |
考点:反比例函数综合题
专题:
分析:首先由一次函数的图象过(x1,y1),(x2,y2)两个不同的点,且满足
=
.可求得k的值,则可求得两个函数的解析式,即可求得点A,B,C的坐标,然后分别从当
=
,即
=
时,△AOB∽△APC与当
=
,即
=
时,△AOB∽△ACP,去分析求解即可求得答案.
| y2-y1 |
| x2-x1 |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AP |
2
| ||
3
|
| 4 |
| AP |
| AB |
| AP |
| AO |
| AC |
2
| ||
| AP |
| 4 | ||
3
|
解答:解:∵一次函数y=kx+2的图象过(x1,y1),(x2,y2)两个不同的点,
∴y1=kx1+2,y2=kx2+2,
∵
=
,
∴
=
=
,
∴k=
,
∴一次函数的解析式为:y=
x+2,反比例函数的解析式为:y=
,
联立
,
解得:
或
(舍去),
∴点C的坐标为:(2,3),
∵一次函数的图象分别与x轴交于点A,与y轴交于点B,
∴A(-4,0),B(0,2),
∴OA=4,OB=2,
∴AB=
=2
,AC=
=3
,
∵∠BAO=∠CAO,
∴当
=
,即
=
时,△AOB∽△APC,
解得:AP=6,
∴点P的坐标为:(2,0);
当
=
,即
=
时,△AOB∽△ACP,
解得:AP=7.5,
∴点P的坐标为:(3.5,0);
∴P点坐标是:(2,0)或(3.5,0).
故答案为:(2,0)或(3.5,0).
∴y1=kx1+2,y2=kx2+2,
∵
| y2-y1 |
| x2-x1 |
| 1 |
| 2 |
∴
| (kx2+2)-(kx1+2) |
| x2-x1 |
| k(x2-x1) |
| x2-x1 |
| 1 |
| 2 |
∴k=
| 1 |
| 2 |
∴一次函数的解析式为:y=
| 1 |
| 2 |
| 6 |
| x |
联立
|
解得:
|
|
∴点C的坐标为:(2,3),
∵一次函数的图象分别与x轴交于点A,与y轴交于点B,
∴A(-4,0),B(0,2),
∴OA=4,OB=2,

∴AB=
| 42+22 |
| 5 |
| 62+32 |
| 5 |
∵∠BAO=∠CAO,
∴当
| AB |
| AC |
| AO |
| AP |
2
| ||
3
|
| 4 |
| AP |
解得:AP=6,
∴点P的坐标为:(2,0);
当
| AB |
| AP |
| AO |
| AC |
2
| ||
| AP |
| 4 | ||
3
|
解得:AP=7.5,
∴点P的坐标为:(3.5,0);
∴P点坐标是:(2,0)或(3.5,0).
故答案为:(2,0)或(3.5,0).
点评:此题考查了反比例函数的性质、一次函数的性质、待定系数法求函数的解析式以及相似三角形的判定与性质.此题难度较大,综合性很强,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
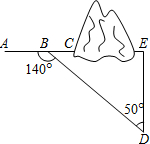 如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°.求开挖点E到点D的距离.
如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°.求开挖点E到点D的距离. 如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )
如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )