题目内容
 如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,sin∠A=
如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,sin∠A=| 3 |
| 5 |
考点:切线的性质
专题:
分析:连接OD,根据切线的性质即可证得BC∥OD,则△ABC∽△AOD,根据相似三角形的性质即可求解.
解答: 解:连接OD.
解:连接OD.
∵AD切半圆O于点D,
∴∠ADO=90°,
∵sinA=
=
,
∴OA=
OD=5,
∴AB=OA-OB=5-3=2.
∵BC⊥AD,即∠BCA=90°,
又∵∠ADO=90°,
∴∠ADO=∠BCA,
∴BC∥OD,
∴
=
,即
=
,
∴BC=
.
故答案是:
.
 解:连接OD.
解:连接OD.∵AD切半圆O于点D,
∴∠ADO=90°,
∵sinA=
| OD |
| AO |
| 3 |
| 5 |
∴OA=
| 5 |
| 3 |
∴AB=OA-OB=5-3=2.
∵BC⊥AD,即∠BCA=90°,
又∵∠ADO=90°,
∴∠ADO=∠BCA,
∴BC∥OD,
∴
| BC |
| OD |
| AB |
| OA |
| BC |
| 3 |
| 2 |
| 5 |
∴BC=
| 6 |
| 5 |
故答案是:
| 6 |
| 5 |
点评:本题考查了切线的性质以及相似三角形的判定与性质,正确判定BC∥OD是关键.

练习册系列答案
相关题目
甲,乙,丙,丁四位选手各10次射击的平均数都是8环,众数和方差如下表,则这四人中水平发挥最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 众数(环) | 9 | 8 | 8 | 10 |
| 方差 | 0.035 | 0.025 | 0.015 | 0.27 |
| A、甲 | B、乙 | C、丙 | D、丁 |
观察下列图形:
它们是按一定规律排列的,依照此规律,第9个图形中共有★( )

它们是按一定规律排列的,依照此规律,第9个图形中共有★( )

| A、16个 | B、18个 |
| C、20个 | D、24个 |

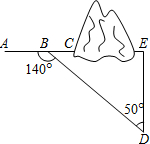 如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°.求开挖点E到点D的距离.
如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°.求开挖点E到点D的距离. 如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )
如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )