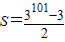题目内容
求3+32+33+…+399的值,我们可以采用如下的方法:设S=3+32+33+…+399①,则3S=32+33+34+…+3100②,由②-①得:2S=3100-3,所以S=
.仿照以上的方法可求得1+5+52+…+52012的值为( )
| 3100-3 |
| 2 |
A.
| B.
| C.
| D.
|
设S=1+5+52+…+52012①,则5S=5+52+…+52013②,
那么②-①,得
4S=52013-1,
∴S=
.
故选B.
那么②-①,得
4S=52013-1,
∴S=
| 52013-1 |
| 4 |
故选B.

练习册系列答案
相关题目
 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题. 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题.