Question

【题目】如图，抛物线的对称轴是直线，且与轴相交于A，B两点（点B在点A的右侧），与轴交于点C．

（1）求抛物线的解析式和A，B两点的坐标；

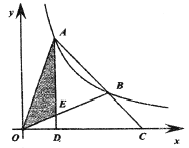
（2）若点P是抛物线上B、C两点之间的一个动点（不与B,C重合），则是否存在一点P，使△BPC的面积最大？若存在，请求出△BPC的最大面积；若不存在，试说明理由．

Answer 1

【答案】（1），点A的坐标为（-2,0），点B的坐标为（8,0）；（2）当=4时，△PBC的面积最大，最大面积是16．

【解析】

(1)由抛物线的对称轴是直线x=3，解出a的值，即可求得抛物线解析式，在令其y值为0，解一元二次方程即可求出A和B的坐标；
(2)易求点C的坐标为(0，4)，设直线BC的解析式为y=kx+b(k≠0)，将B(8，0)，C(0，4)代入y=kx+b，解出k和b的值，即得直线BC的解析式；设点P的坐标为(，)，过点P作PD∥y轴，交直线BC于点D，则点D的坐标为(，)，利用面积公式得出关于x的二次函数，从而求得其最值．

(1)∵抛物线的对称轴是直线，

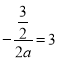∴，解得，

∴ 抛物线的解析式为：，

当时，即，

解之得：， ，

∴点A的坐标为(-2,0)，点B的坐标为(8,0)，

故答案为：，点A的坐标为(-2,0)，点B的坐标为(8,0)；

(2)当时，

∴点C的坐标为(0,4)

设直线BC的解析式为，

将点B(8,0)和点C(0,4)的坐标代入得：

，

解之得：，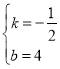

∴直线BC的解析式为，

假设存在，

设点P 的坐标为(，)，

过点P作PD∥轴，交直线BC于点D，交轴于点E，

则点D的坐标为(，)，如图所示，

PD=-()=

∴S△PBC=S△PDC+ S△PDB=

=

=

=

∵-1<0

∴当=4时，△PBC的面积最大，最大面积是16．