题目内容
20.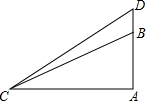 如图,△ABC中,∠A=90°,AC=20,AB=10,延长AB到D,使AC+AB=CD+BD,求BD的长.
如图,△ABC中,∠A=90°,AC=20,AB=10,延长AB到D,使AC+AB=CD+BD,求BD的长.
分析 设BD=x,由AB与AC的长求出AC+AB的值,根据CD+DB=AC+AB求出CD+DB的长,可表示出CD,在直角三角形ACD中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出BD的长.
解答 解:由AC=20,AB=10,得到CD+DB=AC+AB=20+10=30,
设BD=x,则CD=30-x,
在Rt△ACD中,根据勾股定理得(30-x)2=(x+10)2+202,
解得:x=5,
则BD=5.
点评 此题考查了勾股定理,利用了方程的思想,熟练掌握勾股定理的解本题的关键.

练习册系列答案
相关题目
10.下列函数中,反比例函数是( )
| A. | $y=\frac{x}{3}$ | B. | y=$\frac{1}{x+1}$ | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{3x}$ |
15.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组部分统计数据.
(1)根据上表数据计算a=0.251.估计从袋中摸出一个球是黑球的概率是0.25.(精确到0.01)
(2)估算袋中白球的个数.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
| 摸到黑球的频率$\frac{m}{n}$ | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 | a |
(2)估算袋中白球的个数.
10. 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
11.下列性质中,矩形具有但菱形不一定具有的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 对边平行 |
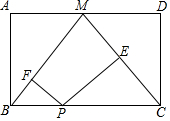 如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.
如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.
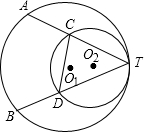 已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.
已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.