题目内容
如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2,﹣)和点C(﹣3,﹣3)两点均在抛物线上,点F(0,﹣)在y轴上,过点(0,)作直线l与x轴平行.
(1)求抛物线的解析式和线段BC的解析式.
(2)设点D(x,y)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线,与抛物线交于点G.设线段GD的长度为h,求h与x之间的函数关系式,并求出当x为何值时,线段GD的长度h最大,最大长度h的值是多少?
(3)若点P(m,n)是抛物线上位于第三象限的一个动点,连接PF并延长,交抛物线于另一点Q,过点Q作QS⊥l,垂足为点S,过点P作PN⊥l,垂足为点N,试判断△FNS的形状,并说明理由;
(4)若点A(﹣2,t)在线段BC上,点M为抛物线上的一个动点,连接AF,当点M在何位置时,MF+MA的值最小,请直接写出此时点M的坐标与MF+MA的最小值.
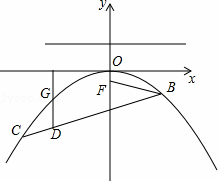
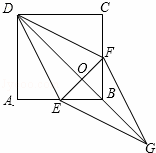
| 解:(1)如图1, ∵抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O, ∴抛物线解析式为y=ax2. ∵点C(﹣3,﹣3)在抛物线y=ax2上, ∴.9a=﹣3. ∴a=﹣. ∴抛物线的解析式为y=﹣x2. 设直线BC的解析式为y=mx+n. ∵B(2,﹣)、C(﹣3,﹣3)在直线y=mx+n上, ∴ 解得: ∴直线BC的解析式为y=x﹣2. (2)如图2, ∵点D(x,y)是线段BC上的一个动点(点D不与B,C重合), ∴yD=x﹣2,且﹣3<x<2. ∵DG⊥x轴, ∴xG=xD=x. ∵点G在抛物线y=﹣x2上, ∴yG=﹣x2. ∴h=DG=yG﹣yD =﹣x2﹣(x﹣2) =﹣x2﹣x+2 =﹣(x2+x)+2 =﹣(x2+x+﹣)+2 =﹣(x+)2+ =﹣(x+)2+ ∵﹣<0,﹣3<﹣<2, ∴当x=﹣时,h取到最大值,最大值为 ∴h与x之间的函数关系式为h=﹣(x+)2+ 当x=﹣时,线段GD的长度h最大,最大长度h的值是 (3)△FNS是直角三角形. 证明:过点F作FT⊥PN,垂足为T,如图3, ∵点P(m,n)是抛物线y=﹣x2上位于第三象限的一个动点, ∴n=﹣m2.m<0,n<0. ∴m2=﹣3n. 在Rt△PTF中, ∵PT=﹣﹣n,FT=﹣m, ∴PF= = = = =﹣n. ∵PN⊥l,且l是过点(0,)平行于x轴的直线, ∴PN=﹣n. ∴PF=PN. ∴∠PNF=∠PFN. ∵PN⊥l,OF⊥l, ∴PN∥OF. ∴∠PNF=∠OFN. ∴∠PFN=∠OFN. 同理可得:∠QFS=∠OFS. ∵∠PFN+∠OFN+∠OFS ∴2∠OFN+2∠OFS=180°. ∴∠OFN+∠OFS=90°. ∴∠NFS=90°. ∴△NFS是直角三角形. (4)过点M作MH⊥l,垂足为H,如图4, 在(3)中已证到PF=PN,由此可得:抛物线y=﹣x2上的点到点F(0,﹣)的距离与到直线y=的距离相等. ∴MF=MH. ∴MA+MF=MA+MH. 由两点之间线段最短可得: 当A、M、H三点共线(即AM⊥l)时,MA+MH(即MA+MF)最小,等于AH. 即xM=xA=﹣2时,MA+MF取到最小值. 此时,yM=﹣×(﹣2)2=﹣,点M的坐标为(﹣2,﹣); yA=×(﹣2)﹣2=﹣,点A的坐标为(﹣2,﹣); MF+MA的最小值=AH=﹣(﹣)= ∴当点M的坐标为(﹣2,﹣)时,MF+MA的值最小,最小值为
|

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案每年4月23日是“世界读 书日”,为了了解某校八年级500名学生对“世界读书日”的知晓情况,从中随机抽取了50名学生进行调查.在这次调查中,样本是( )
书日”,为了了解某校八年级500名学生对“世界读书日”的知晓情况,从中随机抽取了50名学生进行调查.在这次调查中,样本是( )
|
| A. | 500名学生 |
|
| B. | 所抽取的50名学生对“世界读书日”的知晓情况 |
|
| C. | 50名学生 |
|
| D. | 每一名学生对“世界读书日”的知晓情况 |
据省环保网发布的消息,吉首市空气质量评价连续两年居全省14个省辖市城市之最,下表是吉首市2014年5月份前10天的空气质量指数统计表
| (一)2014年5月1日~10日空气质量指数 | ||||||||||
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
| 空气质量指数(AQI) | 28 | 38 | 94 | 53 | 63 | 149 | 53 | 90 | 84 | 35 |
| (二)空气质量污染指数标准(AQI) | |
| 污染指数 | 等级 |
| 0~50 | 优 |
| 51~100 | 良 |
| 101~150 | 轻微污染 |
| 151~200 | 轻度污染 |
(1)请你计算这10天吉首市空气质量指数的平均数,并据此判断这10填吉首市空气质量平均情况属于哪个等级;(用科学计算器计算或笔算,结果保留整数)
(2)按规定,当空气质量指数AQI≤100时,空气质量才算“达标”,请你根据表(一)和表(二)所提供的信息,估计今年(365天)吉首市空气质量“达标”的天数.(结果保留整数)
已知点A(a,2013)与点B(2014,b)关于x轴对称,则a+b的值为( )
|
| A. | ﹣1 | B. | 1 | C. | 2 | D. | 3 |
 .
. .
. +2
+2 .
. ,其中﹣3<x<2;
,其中﹣3<x<2;



 +∠QFS=180°,
+∠QFS=180°, .
.








 (AQI)情况
(AQI)情况
 -3x+1) = 。
-3x+1) = 。