题目内容
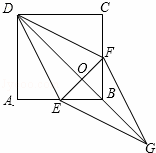
如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交CF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.
1)证明:在正方形ABCD中,AD=CD,∠A=∠C=90°,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF;
(2)四边形DEGF是菱形.
理由如下:在正方形ABCD中,AB=BC,
∵AE=CF,
∴AB﹣AE=BC﹣CF,
即BE=BF,
∵△ADE≌△CDF,
∴DE=DF,
∴BD垂直平分EF,
又∵OG=OD,
∴四边形DEGF是菱形.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
下列运算正确的是( )
|
| A. | a3•a2=a6 | B. | (2a)3=6a3 | C. | (a﹣b)2=a2﹣b2 | D. | 3a2﹣a2=2a2 |
如图,是某公园的一角,∠AOB=90°, 的半径OA长是6米,点C是OA的中点,点D在
的半径OA长是6米,点C是OA的中点,点D在 上,CD∥OB,则图中草坪区(阴影部分)的面积是( )
上,CD∥OB,则图中草坪区(阴影部分)的面积是( )

|
| A. | (3π+ | B. | ( | C. | (3π+9 | D. | ( |
已知x﹣2y=3,则代数式6﹣2x+4y的值为( )
|
| A. | 0 | B. | ﹣1 | C. | ﹣3 | D. | 3 |
若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )
|
| A. | y=(x+2)2+3 | B. | y=(x﹣2)2+3 | C. | y=(x+2)2﹣3 | D. | y=(x﹣2)2﹣3 |
 化简,再求值:(1+
化简,再求值:(1+ )•
)• ,其中x=
,其中x= +1.
+1. )米
)米
 π+
π+ )米
)米 )米
)米 的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=
的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y= 的图象于点C,则△OAC的面积为 .
的图象于点C,则△OAC的面积为 .