Question

将一副三角板按如图的方式摆放在一起，连接AD，求∠ADB的正弦值？

Answer 1

分析：过A点作AE⊥DB，交DB的延长线于点E，构造直角三角形求解．

解答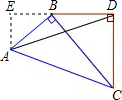：解：过A点作AE⊥DB，交DB的延长线于点E，
则∠ABE=180°-∠ABC-∠DBC=180°-90°-45°=45°，
∴可设AE=BE=x，
∴AB=

x2+x2

=

2

x．
∴BC=AB•tan60°=

6

x．
BD=BC•sin45°=

3

x．
根据勾股定理得：AD=

AE2+DE2

=

5+2 3

x
∴sin∠ADB=

AE

AD

=

x

5+2 3 x

=

5-2 3

13

=

65-26 3

13

．

点评：本题通过构造含有∠ADB的直角三角形，利用直角三角形的性质和锐角三角函数的概念来求解的．