题目内容
6．先化简，再求值：（$\frac{{x}^{2}+4}{2{x}^{2}-4x}$-$\frac{2}{x-2}$）÷$\frac{{x}^{2}-4}{2x}$，其中x是方程$\frac{x-1}{2}$-$\frac{x-2}{5}$=0的解．分析 先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．
解答 解：原式=$\frac{{x}^{2}+4-4x}{2x（x-2）}$÷$\frac{{x}^{2}-4}{2x}$
=$\frac{（x-2）^{2}}{2x（x-2）}$•$\frac{2x}{（x+2）（x-2）}$
=$\frac{1}{x+2}$，
∵$\frac{x-1}{2}$-$\frac{x-2}{5}$=0，
∴x=$\frac{1}{3}$，
∴原式=$\frac{1}{\frac{1}{3}+2}$=$\frac{3}{7}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
画图并回答．
如图，直线y=x+m（m＞0）与x轴交于点A（-2，0），与y轴交于点E，直线y=-x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y=x+m（m＞0）相交于点D，若AB=3，
1．
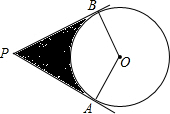如图，过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB，切点为A、B，如果∠APB=60°，则图中阴影的面积等于（ ）
如图，过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB，切点为A、B，如果∠APB=60°，则图中阴影的面积等于（ ）| A． | 12$\sqrt{3}$-4π | B． | 24$\sqrt{3}$-4π | C． | 12$\sqrt{3}$-2π | D． | 24$\sqrt{3}$-2π |
11．下表是我市五个旅游景点7月份某日最高气温（℃）的统计结果．该日这五个旅游景点最高气温的中位数是28℃．
| 景点名称 | 金刀峡 | 缙云山 | 仙女山 | 金佛山 | 黑山谷 |
| 温度（℃） | 32 | 30 | 28 | 24 | 28 |
18．在下列条件中，能画出平行四边形的是（ ）
| A． | 以60cm为一条对角线，20cm和34cm为两条邻边 | |
| B． | 以6cm和10cm为对角线，8cm为一条边 | |
| C． | 以20cm和36cm为对角线，22cm为一条边 | |
| D． | 以6cm为一条对角线，3cm和10cm为两条邻边 |
15．在下列现象中：①时针转动，②电风扇叶片的转动，③转呼啦圈，④传送带上的电视机，其中是旋转的有（ ）
| A． | ①② | B． | ②③ | C． | ①④ | D． | ③④ |