题目内容
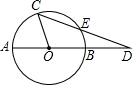 如图,AB是⊙O的直径,D是AB延长线上一点,C是⊙O上一点,CD交⊙O于E,若AB=2DE,∠AOC=72°,则∠D的度数是________度.
如图,AB是⊙O的直径,D是AB延长线上一点,C是⊙O上一点,CD交⊙O于E,若AB=2DE,∠AOC=72°,则∠D的度数是________度.
24
分析:利用了三角形内角和等于180°计算即可知.
解答: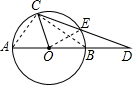 解:连接AC,BC,OE,
解:连接AC,BC,OE,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠AOC=72°,
∴∠CAO= (180°-∠AOC)=
(180°-∠AOC)= (180°-72°)=54°,
(180°-72°)=54°,
∴∠CBD=∠ACB+∠CAO=90°+54°=144°,
∵AB=2DE,
∴∠EDB=∠EOD=2∠BCD,
设∠D=x,则∠BCD= ,
,
∵∠CBD+∠D+∠BCD=180°,
∴x+ +144°=180°,
+144°=180°,
解得x=24°,
∴∠D的度数是24度.
故答案为:24.
点评:①几何计算题中,如果依据题设和相关的几何图形的性质列出方程(或方程组)求解的方法叫做方程的思想;
②求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
③三角形的外角通常情况下是转化为内角来解决.
分析:利用了三角形内角和等于180°计算即可知.
解答:
 解:连接AC,BC,OE,
解:连接AC,BC,OE,∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠AOC=72°,
∴∠CAO=
 (180°-∠AOC)=
(180°-∠AOC)= (180°-72°)=54°,
(180°-72°)=54°,∴∠CBD=∠ACB+∠CAO=90°+54°=144°,
∵AB=2DE,
∴∠EDB=∠EOD=2∠BCD,
设∠D=x,则∠BCD=
 ,
,∵∠CBD+∠D+∠BCD=180°,
∴x+
 +144°=180°,
+144°=180°,解得x=24°,
∴∠D的度数是24度.
故答案为:24.
点评:①几何计算题中,如果依据题设和相关的几何图形的性质列出方程(或方程组)求解的方法叫做方程的思想;
②求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
③三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为