题目内容
15.已知二次函数y=2x2-4x-6.(1)用配方法将y=2x2-4x-6化成y=a (x-h)2+k的形式;并写出对称轴和顶点坐标.
(2)当0<x<4时,求y的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积.
分析 (1)先提取公因式2,然后再利用配方法将原式变形为y=2(x-1)2-8,最后再求得抛物线的对称和顶点坐标即可;
(2)当x=1时,y有最小值,当x=4时,y有最大值,从而可求得y的范围;
(3)先求得抛物线与x轴、y轴的交点坐标,最后,依据三角形的面积公式求解即可.
解答 解:(1)y=2x2-4x-6=2(x2-2x+1-1)-6=2(x2-2x+1)-2-6=2(x-1)2-8,
∴抛物线的对称轴为x=1,顶点坐标为(1,-8).
(2)当x=1时,y有最小值,最小值为-8,
∵0<x<4,
∴y的最大值为10.
∴y的取值范围是-8≤y<10.
(3)当x=0时,y=-6,
当y=0时,2x2-4x-6=0,解得:x=3或x=-1,
∴函数图象与两坐标轴交点所围成的三角形的面积=$\frac{1}{2}$×4×6=12.
点评 本题主要考查的是二次函数的应用,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
10.正比例函数y=3x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
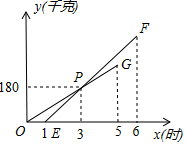 某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象. 如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.
如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.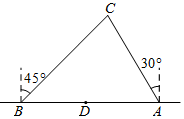 如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.