��Ŀ����
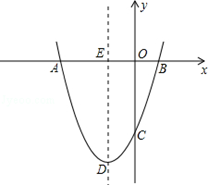
��ͼ�٣������κ��� ��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬��A��������������
��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬��A��������������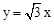 ��ͼ��ĶԳƵ�ΪC��
��ͼ��ĶԳƵ�ΪC��
��1����b��c��ֵ��
��2��֤������C ������Ķ��κ�����ͼ���ϣ�
��3����ͼ�ڣ�����B��DB�ͣ��ύ����������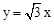 ��ͼ���ڵ�D������AC��������������
��ͼ���ڵ�D������AC��������������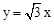 ��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�
��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�
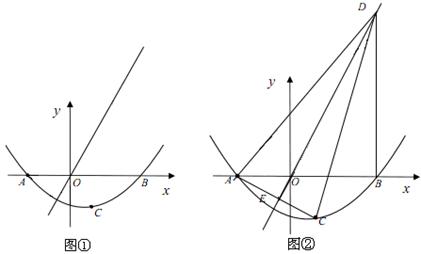
 ��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬��A��������������
��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬��A��������������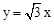 ��ͼ��ĶԳƵ�ΪC��
��ͼ��ĶԳƵ�ΪC����1����b��c��ֵ��
��2��֤������C ������Ķ��κ�����ͼ���ϣ�
��3����ͼ�ڣ�����B��DB�ͣ��ύ����������
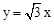 ��ͼ���ڵ�D������AC��������������
��ͼ���ڵ�D������AC��������������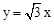 ��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�
��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�
��1��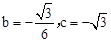 ��
��
��2��������Գƺ�������Ǻ��������C�����꣬����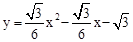 ��֤���ɡ�
��֤���ɡ�
��3������ʱ��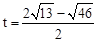 ��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
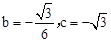 ��
����2��������Գƺ�������Ǻ��������C�����꣬����
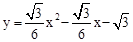 ��֤���ɡ�
��֤���ɡ���3������ʱ��
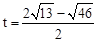 ��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC����������1����A����2,0��,B��3,0���������� ����
 ���������b��c��ֵ��
���������b��c��ֵ����2��������Գƺ�������Ǻ��������C�����꣬����
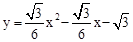 ��֤���ɡ�
��֤���ɡ���3��ͨ��֤����PAE�ס�ECQ�����ʱ��t��
�⣺��1���߶��κ���
 ��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬
��ͼ������ύ�ڵ�A����2,0��,B��3,0�����㣬��
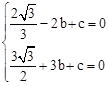 �����
����� ��
����
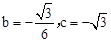 ��
����2��֤�����ɣ�1���ö��κ�������ʽΪ
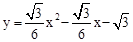 ��
��������������
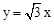 ��ͼ����ȡһ��F
��ͼ����ȡһ��F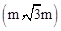 ����FH��x���ڵ�H����
����FH��x���ڵ�H����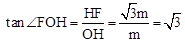 ����
����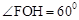 ��
������AC��
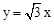 ��ͼ���ڵ�E����CK ��ֱx���ڵ�K��
��ͼ���ڵ�E����CK ��ֱx���ڵ�K��
�ߵ�A����
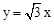 ��ͼ��ĶԳƵ�ΪC��
��ͼ��ĶԳƵ�ΪC����OE��ֱƽ��AC��
��
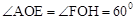 ��OA=2��
��OA=2����
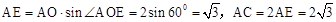 ��
����Rt��ACK����
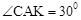 ��
����
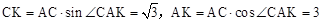 ����
����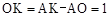 ��
�����C ������Ϊ
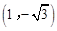 ��
����C
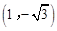 ����
����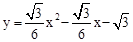 �����=�ұߣ�
�����=�ұߣ����C������Ķ��κ�����ͼ���ϡ�
��3����DB��x�ύ
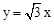 ��ͼ���ڵ�D��B��3,0����
��ͼ���ڵ�D��B��3,0����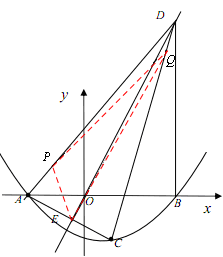
���x=3����
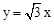 ��
��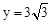 ����BD=
����BD=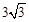 ��
����Rt��ACK��
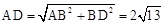 ��
����OE��ֱƽ��AC��
��
 ��
��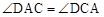 ��
���������ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
��
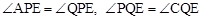 ��
����
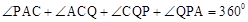 �� ��
�� ��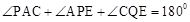 ��
���֡�
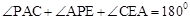 ����
����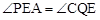 ��
���֡�
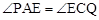 �����PAE�ס�ECQ����
�����PAE�ס�ECQ���� ����
����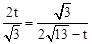 ��
����������
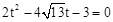 �����
�����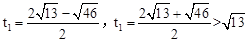 ���������⣬��ȥ����
���������⣬��ȥ���������ʱ��
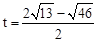 ��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
��ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC��
��ϰ��ϵ�д�
�����Ŀ
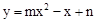 �ĶԳ�����ֱ��x=2��
�ĶԳ�����ֱ��x=2��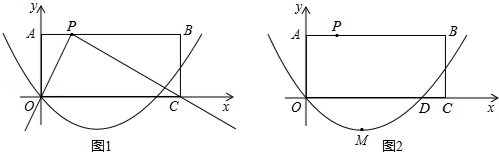
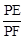 ��ֵ�Ƿ����仯���������仯��˵�����ɣ����������仯�����
��ֵ�Ƿ����仯���������仯��˵�����ɣ����������仯�����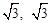 �����Գ���Ϊֱ��
�����Գ���Ϊֱ��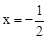 ����P���������ϵ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N�����ı���PMON�Ϸֱ��ȡPC=
����P���������ϵ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N�����ı���PMON�Ϸֱ��ȡPC=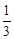 MP��MD=
MP��MD=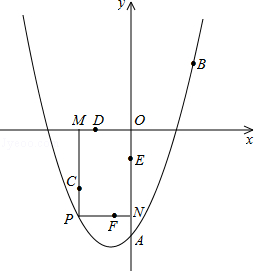
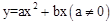 ��
��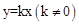 �ϣ����ú�k�Ĵ���ʽ��ʾb��
�ϣ����ú�k�Ĵ���ʽ��ʾb��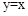 �ϣ�����������Ϊ1��2������n��nΪ����������n��12�����ֱ��ÿ��������x��Ĵ��ߣ������ΪB1��B2��B3������Bn�����߶�AnBnΪ��������������AnBnCnDn������������������һ��������Dn�����������������������α߳���
�ϣ�����������Ϊ1��2������n��nΪ����������n��12�����ֱ��ÿ��������x��Ĵ��ߣ������ΪB1��B2��B3������Bn�����߶�AnBnΪ��������������AnBnCnDn������������������һ��������Dn�����������������������α߳���
 �Ķ���������( )
�Ķ���������( )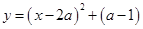 ��
�� ����������
���������� ��
�� ��
��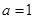 ��
�� ʱ���κ�����ͼ��.���ǵĶ�����һ��ֱ���ϣ�����ֱ�ߵĽ���ʽ��
ʱ���κ�����ͼ��.���ǵĶ�����һ��ֱ���ϣ�����ֱ�ߵĽ���ʽ�� __________________.
__________________.