题目内容
15. 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.(1)小亮行走的总路程是3600m,他途中休息了20min.
(2)求y与x的函数关系式;
(3)当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
分析 (1)根据图象可知小亮走的总路程和中途休息的时间;
(2)根据图象可知y与x的函数关系式分段函数,分三段,根据图象可以求出相应的函数关系;
(3)根据题意可知小颖坐缆车行驶的路程以及所用的时间,从而可以解答本题.
解答 解;(1)根据图象可知:小亮行驶的总路程为3600m,中途休息时间为:50-30=20min.
故答案为;3600,20.
(2)当0≤x≤30时,设y=kx.
∵点(30,1950)在y=kx上,
∴1950=30k.
得,k=65.
∴y=65x.
当30<x<50时,y=1950.
当50≤x≤80时,设y=ax+b.
∵点(50,1950),(80,3600)在y=ax+b上,
∴$\left\{\begin{array}{l}{50a+b=1950}\\{80a+b=3600}\end{array}\right.$
解得,a=55,b=-800.
∴y=55x-800.
由上可得,$y=\left\{\begin{array}{l}{65x(0≤x≤30)}\\{1950(30<x<50)}\\{55x-800(50≤x≤80)}\end{array}\right.$.
(3)∵小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min,
∴小颖行驶的路程为;3600÷2=1800m,行驶的时间为:1800÷180=10min.
∴小颖到达终点,小亮行驶的时间为:50+10=60min.
∴将x=60代入y=55x-800得,y=2500.
∴小亮离缆车终点的路程是:3600-2500=1100m.
点评 本题考查一次函数的应用,分段函数,解题的关键是会看函数图象,能根据图象提供的信息,得出相应的函数解析式.

 名校课堂系列答案
名校课堂系列答案| A. | 某型号节能灯的使用寿命 | B. | 某水库中鱼的种类 | ||
| C. | 某鞋厂生产的鞋底承受的弯折次数 | D. | 某班同学“立定跳远”的成绩 |
| A. | a=-5,b=-3 | B. | a=3,b=3 | C. | a=-3,b=-3 | D. | a=-3,b=3 |
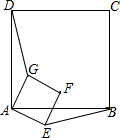 如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.
如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.