题目内容
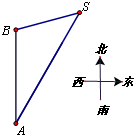
如图,一艘船以每小时30海里的速度向东北方向航行,在A处观测灯塔S在船的北偏东75°的方向,航行12分钟后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘 船可以继续沿东北方向航行吗?为什么?(参考数据:
船可以继续沿东北方向航行吗?为什么?(参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
 解:作与正北方向平行的直线,与SB的延长线相交于点C,过点S作SD⊥AB于D.
解:作与正北方向平行的直线,与SB的延长线相交于点C,过点S作SD⊥AB于D.∵AB=30×
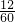 =6(海里),
=6(海里),∵∠CAB=45°,∠ACB=90°,
∴AC=BC=AB•sin45°=6×
 =3
=3 (海里),
(海里),∵∠CAS=75°,∠ACS=90°,
∴SC=AC•tan75°=3
 ×(2+
×(2+ )=6
)=6 +3
+3 (海里),
(海里),∴BS=3
 +3
+3 (海里),
(海里),∵∠DBS=∠ABC=45°,
∴SD=BS•sin45°=(3
 +3
+3 )×
)× =3+3
=3+3 ≈8.2>8,
≈8.2>8,∴这艘船可以继续沿东北方向航行.
分析:问这艘船能否可以继续沿东北方向航行,只要证明D与S的距离要大于8海里,可以做与正北方向平行的直线,与SB的延长线相交于点C.则△ABC,△ACS都是直角三角形,可以运用勾股定理来计算.
点评:此题考查的是对直角三角形勾股定理的运用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 船可以继续沿东北方向航行吗?为什么?(参考数据:
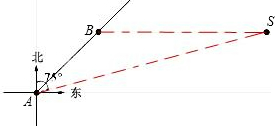
船可以继续沿东北方向航行吗?为什么?(参考数据: 如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)
如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)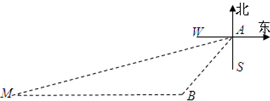 如图,一艘船以每小时40海里的速度向西南方向航行,在A处观测灯塔M在船的南偏西75°的方向,航行9分钟后到达B处,这时灯塔M恰好在船的正西方向.已知距离此灯塔9海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:
如图,一艘船以每小时40海里的速度向西南方向航行,在A处观测灯塔M在船的南偏西75°的方向,航行9分钟后到达B处,这时灯塔M恰好在船的正西方向.已知距离此灯塔9海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据: