题目内容
19.若关于x的方程2x2+3x-m=0有实根,mx2+(2m+1)x+m=0有两个不等实根,那么m应满足的范围是m>-$\frac{1}{4}$且m≠0.分析 根据已知得出32-4×2×(-m)≥0且(2m+1)2-4×m×m>0,m≠0,求出组成的不等式组的解集即可.
解答 解:∵关于x的方程2x2+3x-m=0有实根,mx2+(2m+1)x+m=0有两个不等实根,
∴32-4×2×(-m)≥0且(2m+1)2-4×m×m>0,m≠0,
解得:m>-$\frac{1}{4}$且m≠0,
故答案为:m>-$\frac{1}{4}$且m≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
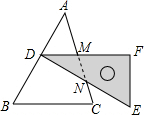 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,且DE⊥AB,∠A=50°,BC∥DF,则∠DNM的度数为40°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,且DE⊥AB,∠A=50°,BC∥DF,则∠DNM的度数为40°.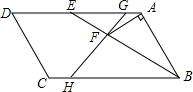 如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.
如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.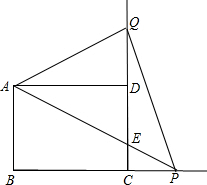 如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.
如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.