题目内容
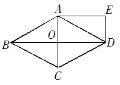
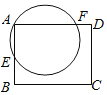
【题目】如图，在矩形ABCD中，过点A的圆O交边AB于点E，交边AD于点F，已知AD=5，AE=2，AF=4．如果以点D为圆心，r为半径的圆D与圆O有两个公共点，那么r的取值范围是______．
【答案】
【解析】
因为以点D为圆心，r为半径的圆D与圆O有两个公共点，则圆D与圆O相交，圆心距满足关系式：|R-r|<d<R+r，求得圆D与圆O的半径代入计算即可.
连接OA、OD，过O点作ON⊥AE，OM⊥AF.
AN=
AE=1，AM=AF=2，MD=AD-AM=3
∵四边形ABCD是矩形
∴∠BAD=∠ANO=∠AMO=90°，
∴四边形OMAN是矩形
∴OM=AN=1
∴OA=
,OD=
∵以点D为圆心，r为半径的圆D与圆O有两个公共点，则圆D与圆O相交
∴
练习册系列答案
相关题目
