Question

【题目】已知圆O的半径长为2，点A、B、C为圆O上三点，弦BC=AO，点D为BC的中点，

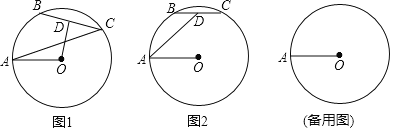
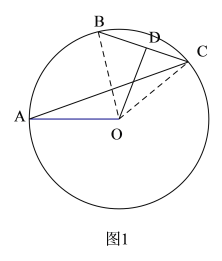
(1)如图，连接AC、OD，设∠OAC=α，请用α表示∠AOD；

(2)如图，当点B为的中点时，求点A、D之间的距离：

(3)如果AD的延长线与圆O交于点E，以O为圆心，AD为半径的圆与以BC为直径的圆相切，求弦AE的长．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）连接OB、OC，可证△OBC是等边三角形，根据垂径定理可得∠DOC等于30°，OA=OC可得∠ACO=∠CAO=α，利用三角形的内角和定理即可表示出∠AOD的值.

（2）连接OB、OC，可证△OBC是等边三角形，根据垂径定理可得∠DOB等于30°，因为点D为BC的中点，则∠AOB=∠BOC=60°，所以∠AOD等于90°，根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD、AD的长.

（3）分两种情况讨论：两圆外切，两圆内切.先根据两圆相切时圆心距与两圆半径的关系，求出AD的长，再过O点作AE的垂线，利用勾股定理列出方程即可求解.

(1)如图1：连接OB、OC.

∵BC=AO

∴OB=OC=BC

∴△OBC是等边三角形

∴∠BOC=60°

∵点D是BC的中点

∴∠BOD=

∵OA=OC

∴=α

∴∠AOD=180°-α-α-=150°-2α

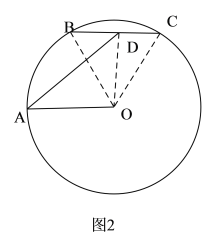
(2)如图2：连接OB、OC、OD.

由（1）可得：△OBC是等边三角形，∠BOD=

∵OB=2，

∴OD=OBcos=

∵B为的中点，

∴∠AOB=∠BOC=60°

∴∠AOD=90°

根据勾股定理得：AD=

（3）①如图3.圆O与圆D相内切时：

连接OB、OC，过O点作OF⊥AE

∵BC是直径，D是BC的中点

∴以BC为直径的圆的圆心为D点

由（2）可得：OD=，圆D的半径为1

∴AD=

设AF=x

在Rt△AFO和Rt△DOF中，

即

解得：

∴AE=

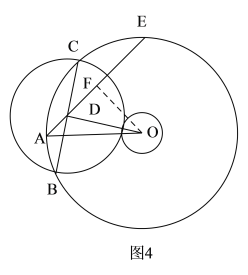
②如图4.圆O与圆D相外切时：

连接OB、OC，过O点作OF⊥AE

∵BC是直径，D是BC的中点

∴以BC为直径的圆的圆心为D点

由（2）可得：OD=，圆D的半径为1

∴AD=

在Rt△AFO和Rt△DOF中，

即

解得：

∴AE=