题目内容
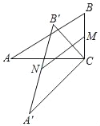
【题目】如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，N是A'B'的中点，连接MN，若BC＝4，∠ABC＝60°，则线段MN的最大值为_____．
【答案】6
【解析】
如图连接CN．由题意可得∠A=30°，根据含30°角的直角三角形性质可得AB的长，根据斜边中线的性质可求出CN=4，根据MN≤CN+CM，可得MN≤6，由此即可得答案.
连接CN．
在Rt△ABC中，∵∠ACB＝90°，BC＝4，∠ABC＝60°，
∴∠A＝30°，
∴AB＝A′B′＝2BC＝8，
∵NB′＝NA′，
∴CN＝
A′B′＝4，
∵CM＝BM＝2，
∴MN≤CN+CM＝6，
∴MN的最大值为6（M、C、N三点共线），
故答案为：6
练习册系列答案
相关题目
【题目】在一次数学测试中，同年级人数相同的甲、乙两个班的成绩统计如下表：
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估，学生的评估结果如下：
这次数学测试成绩中，甲、乙两个班的平均水平相同；
甲班学生中数学成绩95分及以上的人数少；
乙班学生的数学成绩比较整齐，分化较小．
上述评估中，正确的是______
填序号
