题目内容
(14分)
△ABC是边长为4的等边三角形，在射线AB和BC上分别有动点P、Q，且AP=CQ，连结PQ交直线AC于点D，作PE⊥AC，垂足为E.
(1)如图，当点P在边AB(与点A、B不重合)上，问：
①线段PD与线段DQ之间有怎样的大小关系？试证明你的结论.
②随着点P、Q的移动，线段DE的长能否确定？若能，求出DE
的长，若不能，简要说明理由；
(2)当点P在射线AB上，若设AP=x，CD=y，求：
①y与x之间的函数关系式，并写出x的取值范围；
②当x为何值时，△PCQ的面积与△ABC的面积相等．
【答案】
（1）①PD＝DQ，理由略 ②能确定，DE＝2
（2）①y=2－
x (0＜x≤4)或y=x－2(x＞4)
②当0＜x≤4时，无解 当x＞4时，x＝2＋2
【解析】
(1)①PD＝DQ，理由略 ②能确定，DE＝2
(2)①y=2－x (0＜x≤4)或y=x－2(x＞4)
②当0＜x≤4时，无解 当x＞4时，x＝2＋2
练习册系列答案
相关题目
如图己知E、F分别是△ABC的边AC、AB的中点，过A、E、F三点作⊙O的半径是| 1 |
| 4 |
| A、EF | B、AC | C、AB | D、BC |
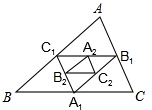（2012•六合区一模）如图，点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点，点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点，依此类推，则△AnBnCn与△ABC的面积比为
时（n为正整数），求△ADnFn的面积Sn，△DnEnFn的面积Sn′．
已知，如图，a，b，c分别是△ABC中∠A，∠B，∠C的对边，P为BC上一点，以AP为直径的圆O交AB于D，PE∥AB交AC于E，b，c是方程x2+kx+9=0的两根，且（b2+c2）（b2+c2-14）-72=0，锐角B的正弦值等于