Question

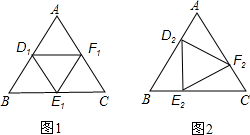
如图1，△ABC为等边三角形，面积为S．D₁，E₁，F₁分别是△ABC三边上的点，且AD₁=BE₁=CF₁=

1

2

AB，连接D₁E₁，E₁F₁，F₁D₁，可得△D₁E₁F₁．
（1）用S表示△AD₁F₁的面积S₁=

1

4

，△D₁E₁F₁的面积S₁′=

1

4

；
（2）当D₂，E₂，F₂分别是等边△ABC三边上的点，且AD₂=BE₂=CF₂=

1

3

AB时，如图②，求△AD₂F₂的面积S₂和△D₂E₂F₂的面积S₂′；
（3）按照上述思路探索下去，当D_n，E_n，F_n分别是等边△ABC三边上的点，且AD_n=BE_n=CF_n=

1

n+1

AB时（n为正整数），求△AD_nF_n的面积S_n，△D_nE_nF_n的面积S_n′．

Answer 1

分析：（1）根据已知条件，可以知道图中四个小三角形都是全等的等边三角形，所以面积相等，每个都是全部的

1

4

；
（2）与上问比较，发现分点的位置由原来的二等分点变成了现在的三等分点，同样易证中间的小三角形是等边三角形，而其余的三个全等，从而得出结果；
（3）与上问比较，只是分点的位置由原来的三等分点变成了（n+1）等分点，所以做法与（2）完全一样．

解答：解：（1）设等边△ABC的边长是a，
∵AD₁=AF₁，∠A=60°，
∴△AD₁F₁是等边三角形，
同理其余三个三角形都是等边三角形，
∴△AD₁F₁≌△BE₁D₁≌△CF₁E₁≌△D₁E₁F₁，
∴S₁=

1

4

S，S₁'=

1

4

S．

（2）设△ABC的边长为a，则△AD₂F₂的面积S2=

1

2

AD2•AF2sin∠A=

1

2

•

1

3

a•

2

3

a•sin60°=

3 a2

9×2

，
又因为△ABC的面积S=

3

4

a2，所以S₂=

2

9

S，
∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，
又∵AD₂=BE₂=CF₂，AF₂=BD₂=CE₂，
由“SAS”得出△AD₂F₂≌△BE₂D₂≌△CF₂E₂，
∴S₂′=S-3S₂=S-3×

2

9

S=

1

3

S．

（3）设△ABC的边长是a，
则S_n=

1

2

•

1

n+1

a•

n

n+1

a•sin60°=

n

(n+1)2

S，
同理证明△AD_nF_n≌△BE_nD_n≌△CF_nE_n，
∴S_n′=S-3×

n

(n+1)2

S=

n2-n+1

(n+1)2

S．

点评：做有规律的题目时，在由特殊到一般的过程中，要善于抓住不变量，找到解题途径．此题比较难，要求学生有比较好的分析问题、解决问题的能力．