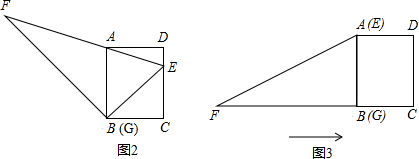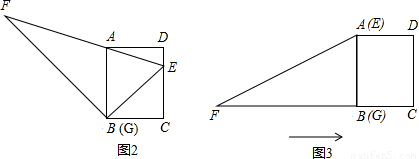Question

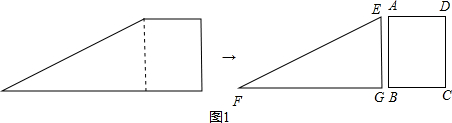
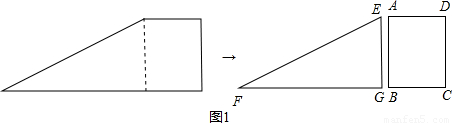
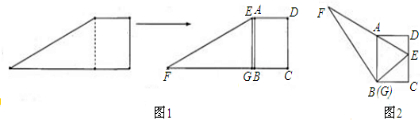
如图1，小明将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2），
（1）求证：∠AED=∠AEB；（2）如果测得AB=5，BC=4，求FG的长．

Answer 1

分析：（1）先根据AB=BE，可知∠BAE=∠AEB，再根据矩形的性质即可得出结论；
（2）由图形旋转的性质可知BE的长，利用勾股定理的求出CE的长，利用相似三角形的性质可判定出△ADE∽△FBE，根据相似三角形的对应边成比例即可得出结论．

解答：解：（1）∵AB=BE=5，
∴∠BAE=∠AEB，（1分）
在矩形ABCD中，AB∥DC，
∴∠BAE=∠AED，（2分）
∴∠AEB=∠AED．（3分）

（2）在Rt△BCE中，BC=4，BE=5，根据勾股定理CE=

52-42

=3，
∴DE=DC-EC=2，（5分）
∵∠AEB=∠AED．∠ADE=∠EBF=90°，
∴△ADE∽△FBE，（7分）
∴

AD

BF

=

DE

BE

，
即BF=

5×4

2

=10．（9分）

点评：本题考查的是相似三角形的判定与性质，图形旋转的性质、矩形的性质及勾股定理，涉及面较广，难易适中．