题目内容
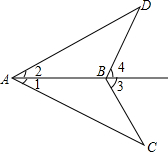 如图,已知∠1=∠2,∠3=∠4,说出下列判断成立的理由:
如图,已知∠1=∠2,∠3=∠4,说出下列判断成立的理由:(1)△ABC≌△ABD;
(2)AC=AD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由∠3=∠4,可得∠ABC=∠ABD,利用ASA即可证明△ABC≌△ABD;
(2)由(1)中的全等三角形性质即可得到AC=AD.
(2)由(1)中的全等三角形性质即可得到AC=AD.
解答:证明:(1)∵∠3=∠4,
∴∠ABC=∠ABD,
在△ABC和△ABD中,
,
∴△ABC≌△ABD(ASA);
(2)∵△ABC≌△ABD,
∴AC=AD.
∴∠ABC=∠ABD,
在△ABC和△ABD中,
|
∴△ABC≌△ABD(ASA);
(2)∵△ABC≌△ABD,
∴AC=AD.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.全等三角形的对应边相等,对应角相等.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图所示,在⊙O中,∠AOB=70°,则∠ACB=( )
如图所示,在⊙O中,∠AOB=70°,则∠ACB=( )| A、70° | B、140° |
| C、35° | D、30° |
把160元的电器连续两次降价后的价格为y元,若平均每次降价的百分率是x,则y与x的函数关系式为( )
| A、y=320(x-1) |
| B、y=320(1-x) |
| C、y=160(1-x2) |
| D、y=160(1-x)2 |
已知两圆半径长是方程x2-9x+14=0的两个根,若圆心距是5,则两圆的位置关系是( )
| A、内切 | B、相交 | C、外切 | D、外离 |
下列计算正确的是( )
| A、-1+1=0 | ||
| B、-2-2=0 | ||
C、4÷
| ||
| D、-|-5|=5 |
 如图,∠1=∠2,∠BAE=∠CAE,求证:△BAE≌△CAE.
如图,∠1=∠2,∠BAE=∠CAE,求证:△BAE≌△CAE.