题目内容
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 |
| 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
解:(1)经销商能盈利=5×11+5×17+5×9+5×13=5×50=250;
(2)设甲店配A种水果x箱,则甲店配B种水果(10﹣x)箱,
乙店配A种水果(10﹣x)箱,乙店配B种水果10﹣(10﹣x)=x箱.
∵9×(10﹣x)+13x≥100,
∴x≥2 ,
,
经销商盈利为w=11x+17•(10﹣x)+9•(10﹣x)+13x=﹣2x+260.
∵﹣2<0,
∴w随x增大而减小,
∴当x=3时,w值最大.
甲店配A种水果3箱,B种水果7箱.乙店配A种水果7箱,B种水 果3箱.最大盈利:﹣2×3+260=254(元).
果3箱.最大盈利:﹣2×3+260=254(元).

下列说法错误的是( )
|
| A. | “伊利”纯牛奶消费者服务热线是4008169999,该十个数的中位数为7 |
|
| B. | 服装店老板最关心的是卖出服装的众数 |
|
| C. | 要了解全市初三近4万名学生2015年中考数学成绩情况,适宜采用全面调查 |
|
| D. | 条形统计图能够显示每组中的具体数据,易于比较数据之间的差别 |
如图,几何体上半部为正三棱柱,下半部为圆柱,其俯视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
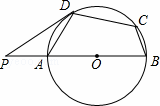
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
|
| A. | 40° | B. | 35° | C. | 30° | D. | 45° |
 钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).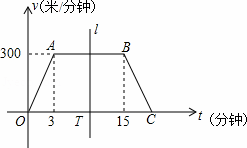
 ﹣(π﹣1)0﹣4sin45°;
﹣(π﹣1)0﹣4sin45°;



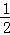 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.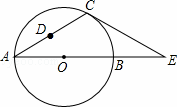
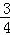 x上,则点B与其对应点B′间的距离为 .
x上,则点B与其对应点B′间的距离为 .