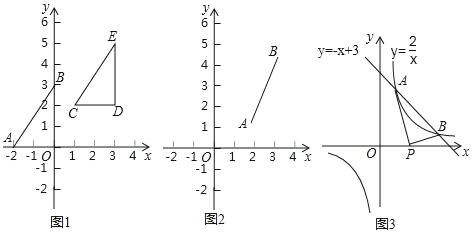Question

【题目】已知抛物线的顶点在第一象限，过点作轴于点，是线段上一点（不与点、重合），过点作轴于点，并交抛物线于点．

（1）求抛物线顶点的纵坐标随横坐标变化的函数解析式，并直接写出自变量的取值范围；

（2）若直线交轴的正半轴于点，且，求的面积的取值范围．

Answer 1

【答案】（1）函数解析式为y=x+4（x＞0）；（2）0≤S≤．

【解析】

（1）抛物线解析式为y=-x2+2mx-m2+m+4，设顶点的坐标为（x，y），利用抛物线顶点坐标公式得到x=m，y=m-4，然后消去m得到y与x的关系式即可．

（2）如图，根据已知得出OE=4-2m，E（0，2m-4），设直线AE的解析式为y=kx+2m-4，代入A的坐标根据待定系数法求得解析式，然后联立方程求得交点P的坐标，根据三角形面积公式表示出S=（4-2m）（m-2）=-m2+3m-2=-（m-）2+，即可得出S的取值范围．

（1）由抛物线y=-x2+2mx-m2+m+4可知，a=-1，b=2m，c=-m2+m+4，

设顶点的坐标为（x，y），

∴x=-=m，

∵b=2m，

y=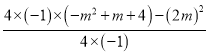=m+4=x+4，

即顶点的纵坐标随横坐标变化的函数解析式为y=x+4（x＞0）；

（2）如图，由抛物线y=-x2+2mx-m2+m+4可知顶点A（m，m+4），

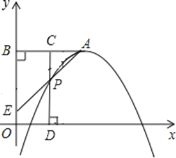
∵轴

∴轴

∴△ACP∽△ABE，

∴

∵

∴，

∵AB=m，

∴BE=2m，

∵OB=4+m，

∴OE=4+m-2m=4-m，

∴E（0，4-m），

设直线AE的解析式为y=kx+4-m，

代入A的坐标得，m+4=km+4-m，解得k=2，

∴直线AE的解析式为y=2x+4-m，

解

得，，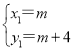

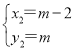∴P（m-2，m），

∴S=（4-m）（m-2）=-m2+3m-2=-（m-3）2+，

∴S有最大值，

∴△OEP的面积S的取值范围：0≤S≤．