题目内容
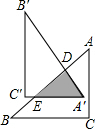 (2012•河南)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是
(2012•河南)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是6
6
.分析:在Rt△ABC中,由勾股定理求得AB=10,由旋转的性质可知AD=A′D,设AD=A′D=BE=x,则DE=10-2x,根据旋转90°可证△A′DE∽△ACB,利用相似比求x,再求△A′DE的面积.
解答:解:Rt△ABC中,由勾股定理求AB=
=10,
由旋转的性质,设AD=A′D=BE=x,则DE=10-2x,
∵△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,
∴∠A′=∠A,∠A′DE=∠C=90°,
∴△A′DE∽△ACB,
∴
=
,即
=
,解得x=3,
∴S△A′DE=
DE×A′D=
×(10-2×3)×3=6,
故答案为:6.
| AC2+BC2 |
由旋转的性质,设AD=A′D=BE=x,则DE=10-2x,
∵△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,
∴∠A′=∠A,∠A′DE=∠C=90°,
∴△A′DE∽△ACB,
∴
| DE |
| A′D |
| BC |
| AC |
| 10-2x |
| x |
| 8 |
| 6 |
∴S△A′DE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:6.
点评:本题考查了相似三角形的判定与性质,勾股定理及旋转的性质.关键是根据旋转的性质得出相似三角形,利用相似比求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•河南)如图所示的几何体的左视图是( )
(2012•河南)如图所示的几何体的左视图是( ) ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2012•河南)如图,已知AB是⊙O的直径,AD切⊙O于点A,
(2012•河南)如图,已知AB是⊙O的直径,AD切⊙O于点A,
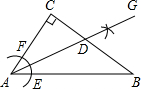 (2012•河南)如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于
(2012•河南)如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于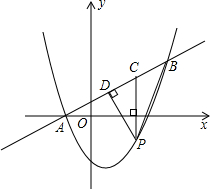 (2012•河南)如图,在平面直角坐标系中,直线y=
(2012•河南)如图,在平面直角坐标系中,直线y=